题目内容
某家具厂根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产A、B、C三种型号的沙发共120套,且C型号沙发至少生产20套.已知生产这些沙发每套所需工时和每套产值如表:
问每周应生产A、B、C型号的沙发各多少套,才能使产值最高?最高产值是多少?(以千元为单位)
| 沙发型号 | A型号 | B型号 | C型号 | ||||||
| 工时 |
|
|
| ||||||
| 产值/千元 | 4 | 3 | 2 |
考点:简单线性规划
专题:不等式的解法及应用
分析:设出变量,建立约束条件和目标函数,利用线性规划的知识即可得到结论.
解答:
 解:设每周生产A型号沙发x套,B型号沙发y套,则生产C型号沙发120-x-y套,产值为z.
解:设每周生产A型号沙发x套,B型号沙发y套,则生产C型号沙发120-x-y套,产值为z.
目标函数为z=4x+3y+2(120-x-y)=2x+y+240,
题目中包含的约束条件为
,即
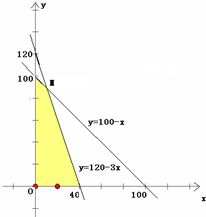
可行域如图所示
可得M(10,90),
所以zmax=2×10+90+240=350(千元)
答:每周应生产A、B、C型号的沙发分别为10套、90套、20套,才能使产值最高,最高产值是350千元.
 解:设每周生产A型号沙发x套,B型号沙发y套,则生产C型号沙发120-x-y套,产值为z.
解:设每周生产A型号沙发x套,B型号沙发y套,则生产C型号沙发120-x-y套,产值为z.目标函数为z=4x+3y+2(120-x-y)=2x+y+240,
题目中包含的约束条件为
|
|
可行域如图所示
可得M(10,90),
所以zmax=2×10+90+240=350(千元)
答:每周应生产A、B、C型号的沙发分别为10套、90套、20套,才能使产值最高,最高产值是350千元.
点评:本题主要考查线性规划的应用,建立约束条件和目标函数是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
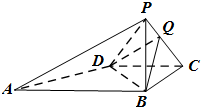 已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=
已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=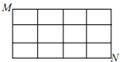 如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有
如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有