题目内容
如图,在棱长为1的正方体ABCD-A1B1C1D1的面对角线B1D1上一点E满足D1E=1,则∠CDE的大小为 .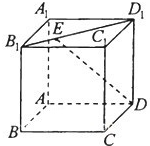

考点:棱柱的结构特征
专题:空间角
分析:首先,建立空间直角坐标系,然后,写出C(1,1,0),D(0,1,0),E(
,1-
,1)的坐标,从而得到
=(1,0,0),
=(
,-
,1),然后,借助于空间中两向量的夹角公式进行求解.
| ||
| 2 |
| ||
| 2 |
| DC |
| DE |
| ||
| 2 |
| ||
| 2 |
解答:
解:如图示:

∵D1E=1,
在直角三角形DD1E中,
∵D1D=D1E=1,
∴DE=
,
以A为坐标原点,以向量
所在直线为x轴,以向量
所在直线为轴,
以向量
所在直线为z轴,建立空间直角坐标系A-xyz,
则C(1,1,0),D(0,1,0),E(
,1-
,1),
∴
=(1,0,0),
=(
,-
,1),
∴cos∠CDE=
=
=
,
∵∠CDE∈[0,π],
∴∠CDE=60°,
故答案为:60°.

∵D1E=1,
在直角三角形DD1E中,
∵D1D=D1E=1,
∴DE=
| 2 |
以A为坐标原点,以向量
| AB |
| AD |
以向量
| AA1 |
则C(1,1,0),D(0,1,0),E(
| ||
| 2 |
| ||
| 2 |
∴
| DC |
| DE |
| ||
| 2 |
| ||
| 2 |
∴cos∠CDE=
| ||||
|
|
1×
| ||||||||||
|
| 1 |
| 2 |
∵∠CDE∈[0,π],
∴∠CDE=60°,
故答案为:60°.
点评:本题重点考查了空间直角坐标系的建立,空间中角度的求解方法等知识,属于中档题.

练习册系列答案
相关题目
 如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )
如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )| A、100米 | ||
B、50
| ||
C、50
| ||
D、50(
|