题目内容
已知等差数列{an}的前n项和为Sn，且满足a2+a4=-22，a1+a4+a7=-21，则使Sn达到最小值的n是 ．
考点：等差数列的性质
专题：等差数列与等比数列
分析：由题意可得首项和公差的方程组，解之可得Sn，由二次函数的知识可得．
解答：
解：设等差数列{an}的公差为d，
则a2+a4=2a1+4d=-22，
a1+a4+a7=3a1+9d=-21，
联立解得a1=-19，d=4，
∴Sn=na1+
d
=-19n+2n2-2n=2n2-21n，
由二次函数的知识可知对称轴为-
=
，
故当n=5时，Sn取到最小值
故答案为：5
则a2+a4=2a1+4d=-22，
a1+a4+a7=3a1+9d=-21，
联立解得a1=-19，d=4，
∴Sn=na1+
| n(n-1) |
| 2 |
=-19n+2n2-2n=2n2-21n，
由二次函数的知识可知对称轴为-
| -21 |
| 2×2 |
| 21 |
| 4 |
故当n=5时，Sn取到最小值
故答案为：5
点评：本题考查等差数列的性质，涉及二次函数的最值，属中档题．
练习册系列答案
相关题目
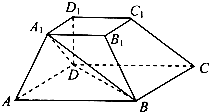如图，在四棱台ABCD-A1B1C1D1中，底面ABCD是平行四边形，DD1⊥平面ABCD，AB=2AD，AD=A1B1，∠BAD=60°．