题目内容
已知z是虚数,且z+
是实数,求证
是纯虚数.
| 1 |
| z |
| z-1 |
| z+1 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:设出虚数z,利用z+
是实数,推出关系式,然后化简所求的表达式,推出是纯虚数即可.
| 1 |
| z |
解答:
证明:设虚数z=a+bi,(b≠0).
z+
=a+bi+
=a+
+(b-
)i.∵z+
是实数,∴b-
=0,∵b≠0可得a2+b2=1.
=
=
=
=
.
显然
是纯虚数.
z+
| 1 |
| z |
| 1 |
| a+bi |
| a |
| a2+b2 |
| b |
| a2+b2 |
| 1 |
| z |
| b |
| a2+b2 |
| z-1 |
| z+1 |
| a-1+bi |
| a+1+bi |
| [(a-1)+bi][(a+1)-bi] |
| (a+1)2+b2 |
| (a2+b2-1)+2bi |
| (a+1)2+b2 |
| 2bi |
| (a+1)2+b2 |
显然
| z-1 |
| z+1 |
点评:本题考查复数的代数形式的混合运算,复数的基本概念,基本知识的考查.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
函数y=
-
+3的定义域是( )
| 5-x |
| x+2 |
| A、-2≤x≤5 |
| B、-5≤x≤2 |
| C、{-2,5} |
| D、{x|-2≤x≤5} |
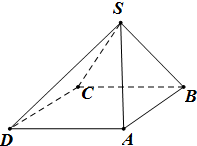 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠ABC=45°,AB=2,BC=2