题目内容
已知函数f(x)=ax2-2ax+2+b(a>0),若f(x)在区间[0,3]上有最大值10,最小值2.
(1)求a,b的值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
(1)求a,b的值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)首先判断出f(x)的对称轴方程,找出它的最大值、最小值,列出方程,即可求出a,b的值;
(2)根据g(x)=f(x)-mx在[2,4]上是单调函数,判断出其对称轴的范围,然后求出m的取值范围即可.
(2)根据g(x)=f(x)-mx在[2,4]上是单调函数,判断出其对称轴的范围,然后求出m的取值范围即可.
解答:
解:(1)函数f(x)=ax2-2ax+2+b(a>0)的对称抽方程是x=1,a>0,
∴f(x)min=f(1),f(x)max=f(3),
即
,
解得a=2,b=2;
(2)由(1)知:f(x)=2x2-4x+4
∴g(x)=2x2-(4+m)x+4
对称轴为:x=
∵g(x)=f(x)-mx在[2,4]上是单调函数,
∴
≤2或
≥4
解得m≤4或m≥12,
综上,m≤4或m≥12.
∴f(x)min=f(1),f(x)max=f(3),
即
|
解得a=2,b=2;
(2)由(1)知:f(x)=2x2-4x+4
∴g(x)=2x2-(4+m)x+4
对称轴为:x=
| 4+m |
| 4 |
∵g(x)=f(x)-mx在[2,4]上是单调函数,
∴
| 4+m |
| 4 |
| 4+m |
| 4 |
解得m≤4或m≥12,
综上,m≤4或m≥12.
点评:此题主要考查了二次函数的性质及其运用,考查了函数单调性的运用,属于中档题.

练习册系列答案
相关题目
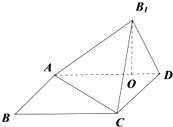 已知四边形ABCD是矩形,AB=
已知四边形ABCD是矩形,AB=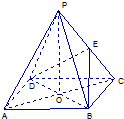 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.