题目内容
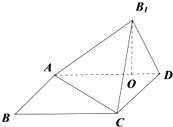已知四边形ABCD是矩形，AB=| 2 |
| 6 |
（1）求证：AB1⊥平面B1CD；
（2）求三棱锥B1-ABC的体积VB1-ABC．
考点：棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题：计算题,空间位置关系与距离
分析：（1）利用线面垂直的判定，AB1⊥CD，又AB1⊥B1C，且B1C∩CD=C∴AB1⊥平面B1CD；（2）AB1⊥平面B1CD，AB1即棱锥的高，后算出底面ABC的面积，代人棱锥体积公式计算．
解答：
解：（1）B1O⊥平面ABCD，CD?平面ABCD，
∴B1O⊥CD，又CD⊥AD，AD∩B1O=O
∴CD⊥平面AB1D，又AB1?平面AB1D
∴AB1⊥CD，又AB1⊥B1C，且B1C∩CD=C
∴AB1⊥平面B1CD； …（6分）
（2）由于AB1⊥平面B1CD，B1D?平面ABCD，∴AB1⊥B1D，
在Rt△AB1D中，B1D=
=2，
又由B1O•AD=AB1•B1D 得B1O=
=
，
∴VB1-ABC=
S△ABC•B1O=
×
×
=
…12分
∴B1O⊥CD，又CD⊥AD，AD∩B1O=O
∴CD⊥平面AB1D，又AB1?平面AB1D
∴AB1⊥CD，又AB1⊥B1C，且B1C∩CD=C
∴AB1⊥平面B1CD； …（6分）
（2）由于AB1⊥平面B1CD，B1D?平面ABCD，∴AB1⊥B1D，
在Rt△AB1D中，B1D=
| AD2-AB12 |
又由B1O•AD=AB1•B1D 得B1O=
| AB1•B1D |
| AD |
2
| ||
| 3 |
∴VB1-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
点评：本题考查的知识点是直线与平面垂直的判定，棱锥的体积，其中（1）的关键是熟练掌握线面垂直，线面垂直及线线垂直的相互转化，（2）的关键是判断出棱锥的高和底面面积．
练习册系列答案
相关题目