题目内容
13.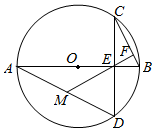 如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.
如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.
分析 由弦CD⊥AB,EF⊥BC,∠A=∠C,得到ME=MD,再由∠D+∠A=∠AEM+∠DEM=90°,能证明M为AD中点.
解答 证明:∵AB为⊙O的直径,弦CD垂直AB于点E,
线段EF垂直于BC,并反向延长交AD于点M,
∴弦CD⊥AB,EF⊥BC,
∴∠D+∠A=∠CEF+∠C=90°,
又∵∠A=∠C,∴∠CEF=∠D=∠DEM,
∴ME=MD,
又∵∠D+∠A=∠AEM+∠DEM=90°,
∴∠A=∠AEM,
∴ME=MA,∴M为AD中点.
点评 本题考查点为线段中点的证明,是中档题,解题时要认真审题,注意垂径定理的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
4.如果等差数列{an}中,a3+a5=8,那么a2+a3+a4+a5+a6=( )
| A. | 21 | B. | 20 | C. | 14 | D. | 35 |
18.设命题p:x2=3x+4,q:x=$\sqrt{3x+4}$,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分又不必要条件 |
5.“x≥3”是“x>3”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.函数y=2-|x|-m的图象与x轴有交点时,则( )
| A. | -1≤m<0 | B. | 0≤m≤1 | C. | 0<m≤1 | D. | m≥0 |