题目内容
3.已知圆C经过抛物线y=x2-4x+3与坐标轴的三个交点.(1)求圆C的方程;
(2)设直线2x-y+2=0与圆C交于A,B两点,求|AB|.
分析 (1)求出抛物线y=x2-4x+3与坐标轴的交点坐标,确定圆心与半径,即可求圆C的方程;
(2)利用点到直线的距离公式求出圆心到直线的距离,再由圆的半径,利用垂径定理及勾股定理即可求出|AB|的长.
解答 解:(1)抛物线y=x2-4x+3与坐标轴的交点分别是(1,0),(3,0),(0,3)…(3分)
所求圆的圆心是直线y=x与x=2的交点(2,2),圆的半径是$\sqrt{5}$,
于是圆C的方程为(x-2)2+(y-2)2=5.…(6分)
(2)圆心C到直线2x-y+2=0的距离d=$\frac{4}{\sqrt{5}}$…(9分)
|AB|=2$\sqrt{5-\frac{16}{5}}$=$\frac{6\sqrt{5}}{5}$…(12分)
点评 此题考查了圆C的方程,考查直线与圆相交的性质,涉及的知识有:点到直线的距离公式,圆的标准方程,垂径定理,以及勾股定理,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目
14.下列函数中,与函数y=$\frac{1}{{\sqrt{x}}}$有相同定义域的是( )
| A. | f(x)=lnx | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=|x| | D. | f(x)=ex |
18.设l是空间一条直线,α和β是两个不同的平面,则下列结论正确的是( )
| A. | 若l∥α,l∥β,则α∥β | B. | 若α⊥β,l∥α,则l⊥β | C. | 若α⊥β,l⊥α,则l∥β | D. | 若l∥α,l⊥β,则α⊥β |
8.在锐角△ABC中,角A、B、C所对的边分别为a、b、c,已知a=2,A=2B,那么b的取值范围是( )
| A. | (0,$\sqrt{2}$) | B. | (1,2) | C. | ($\frac{2\sqrt{3}}{3}$,2) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
15.已知a、b、c分别为△ABC三个内角A、B、C所对的边长,∠A=60°,且acosB-bcosA=$\frac{3}{5}$c,则$\frac{2absinC}{{a}^{2}+{b}^{2}-{c}^{2}}$=( )
| A. | -5$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
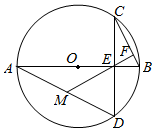 如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.
如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.