题目内容
1.设函数f(x)=k•ax-a-x(a>0且a≠1)是奇函数.(1)求常数k的值;
(2)若$f(1)=\frac{8}{3}$,且函数g(x)=a2x-a-2x-2mf(x)在区间[1,+∞)上的最小值为-2,求实数m的值.
分析 (1)方法一、由奇函数的性质:f(0)=0,解方程可得k=1,检验成立;方法二、运用奇函数的定义,由恒等式的性质即可得到k=1;
(2)求得a=3,即有g(x)=32x-3-2x-2m(3x-3-x),令t=3x-3-x,则t是关于x的增函数,可得$t≥3-\frac{1}{3}=\frac{8}{3}$,h(t)=t2-2mt+2=(t-m)2+2-m2,讨论对称轴和区间的关系,运用单调性,可得最小值,解方程可得m的值.
解答 (1)解法一:函数f(x)=k•ax-a-x的定义域为R,
f(x)是奇函数,所以f(0)=k-1=0,即有k=1.
当k=1时,f(x)=ax-a-x,f(-x)=a-x-ax=-f(x),
则f(x)是奇函数,故所求k的值为1;
解法二:函数f(x)=k•ax-a-x的定义域为R,
由题意,对任意x∈R,f(-x)=-f(x),
即k•a-x-ax=a-x-k•ax,(k-1)(ax+a-x)=0,
因为ax+a-x>0,所以,k=1.
(2)由$f(1)=\frac{8}{3}$,得$a-\frac{1}{a}=\frac{8}{3}$,解得a=3或$a=-\frac{1}{3}$(舍).
所以g(x)=32x-3-2x-2m(3x-3-x),
令t=3x-3-x,则t是关于x的增函数,$t≥3-\frac{1}{3}=\frac{8}{3}$,
g(x)=h(t)=t2-2mt+2=(t-m)2+2-m2,
当$m<\frac{8}{3}$时,则当$t=\frac{8}{3}$时,$g{(x)_{min}}={({\frac{8}{3}})^2}-2m×\frac{8}{3}+2=-2$,
解得$m=\frac{25}{12}$;
当$m≥\frac{8}{3}$时,则当t=m时,$g{(x)_{min}}=2-{m^2}=-2$,m=±2(舍去).
综上,$m=\frac{25}{12}$.
点评 本题考查奇函数的定义和性质的运用,考查可化为二次函数的最值的求法,注意运用换元法和二次韩寒说的对称轴和区间的关系,考查运算能力,属于中档题.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| A. | (-∞,3] | B. | (-∞,3) | C. | (3,+∞) | D. | [3,+∞) |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$i | D. | $\frac{1}{2}$i |
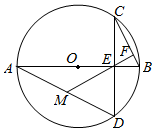 如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.
如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.