题目内容
2.函数y=2-|x|-m的图象与x轴有交点时,则( )| A. | -1≤m<0 | B. | 0≤m≤1 | C. | 0<m≤1 | D. | m≥0 |
分析 根据指数函数的图象与性质,进行转化与解答即可.
解答 解:y=2-|x|-m=($\frac{1}{2}$)|x|-m,
若函数y=2-|x|-m的图象与x轴有交点,
即y=2-|x|-m=($\frac{1}{2}$)|x|-m=0有解,
即m=($\frac{1}{2}$)|x|有解,
∵0<($\frac{1}{2}$)|x|≤1,
∴0<m≤1,
故选:C.
点评 本题考查了函数与方程的应用问题,根据指数函数的图象与性质是解题的关键.

练习册系列答案
相关题目
14.下列函数中,与函数y=$\frac{1}{{\sqrt{x}}}$有相同定义域的是( )
| A. | f(x)=lnx | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=|x| | D. | f(x)=ex |
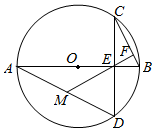 如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.
如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.