题目内容
8.已知等比数列{an}的首项a1=2015,公比为q=$\frac{1}{2}$,记bn=a1a2a3…an,则bn达到最大值时,n的值为( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
分析 由已知${a}_{n}=2015×(\frac{1}{2})^{n-1}$,bn达到最大值时,$\left\{\begin{array}{l}{{a}_{n}≥1}\\{{a}_{n+1}<1}\end{array}\right.$,由此能求出bn达到最大值时,n的值.
解答 解:∵等比数列{an}的首项a1=2015,公比为q=$\frac{1}{2}$,
∴${a}_{n}=2015×(\frac{1}{2})^{n-1}$,
∵bn=a1a2a3…an,∴bn达到最大值时,$\left\{\begin{array}{l}{{a}_{n}≥1}\\{{a}_{n+1}<1}\end{array}\right.$,
∵${a}_{11}=2015×(\frac{1}{2})^{10}$=$\frac{2015}{1024}$>1,${a}_{12}=2015×(\frac{1}{2})^{11}=\frac{2015}{2048}$<1,
∴bn达到最大值时,n的值为11.
故选:B.
点评 本题考查满足的等比数列的项数的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
18.设l是空间一条直线,α和β是两个不同的平面,则下列结论正确的是( )
| A. | 若l∥α,l∥β,则α∥β | B. | 若α⊥β,l∥α,则l⊥β | C. | 若α⊥β,l⊥α,则l∥β | D. | 若l∥α,l⊥β,则α⊥β |
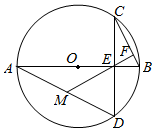 如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.
如图,已知AB为⊙O的直径,弦CD垂直AB于点E,线段EF垂直于BC,并反向延长交AD于点M.证明:M为AD中点.