如果等差数列{an}中.a3+a5=8.那么a2+a3+a4+a5+a6=( )A．21B．20C．14D．35 题目和参考答案——青夏教育精英家教网—

题目内容

4．如果等差数列{a_n}中，a₃+a₅=8，那么a₂+a₃+a₄+a₅+a₆=（　　）

A．

B．

C．

D．

分析由条件利用等差数列的性质求得a₄=4，再根据a₂+a₃+a₄+a₅+a₆=5a₄，运算求得结果．

解答解：∵等差数列{a_n}中，a₃+a₅=8，则a₄=4，
∴a₂+a₃+a₄+a₅+a₆=$\frac{5（{a}_{2}+{a}_{6}）}{2}=5{a}_{4}=20$．
故选：B．

点评本题主要考查等差数列的通项公式，是基础题．

练习册系列答案

同步解析与测评初中总复习指导与训练系列答案

15．已知{a_n}是等差数列，且a₅+a₆=12，则a₂+a₉=（　　）

12．已知m∈R，则直线（m-1）x+（2m-1）y=m-4与圆x²+y²-10x+4y+20=0的位置关系为相交．

19．若不等式a≤x²-4x对任意x∈（0，3]恒成立，则a的取值范围是a≤-4．

9．函数y=log₃（3-x）的定义域为（　　）

16．从编号为001，002，…，800的800个产品中用系统抽样的方法抽取一个样本，已知样本中最小的两个编号分别为008，033，则样本中最大的编号应该是783．

13．

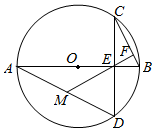如图，已知AB为⊙O的直径，弦CD垂直AB于点E，线段EF垂直于BC，并反向延长交AD于点M．证明：M为AD中点．

14．下列函数中，与函数y=$\frac{1}{{\sqrt{x}}}$有相同定义域的是（　　）

试题分类