题目内容
已知x∈(0,π),且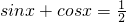 ,求:
,求:
(1)sinx-cosx的值;
(2)sin2x+cos2x的值.
解:(1)∵sinx+cosx= ,
,
∴(sinx+cosx)2= ,
,
即1+2sinxcosx= ,
,
∴2sinxcosx=- ,
,
∴(sinx-cosx)2=1-2sinxcosx=1+ =
= ,
,
又x∈(0,π),
∴sinx>0,cosx<0,
∴sinx-cosx>0,
sinx-cosx= ;
;
(2)∵sinx+cosx= ,sinx-cosx=
,sinx-cosx= ;
;
∴sinx= ,cosx=
,cosx= ,
,
∴cos2x=cos2x-sin2x= -
- =-
=- ,
,
∴sin2x+cos2x=- -
- =-
=-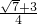 .
.
分析:(1)依题意可知 <x<π,从而可求得sinx-cosx的值;
<x<π,从而可求得sinx-cosx的值;
(2)可求得sinx,cosx的值后,利用二倍角公式可求得sin2x,cos2x的值,继而可得sin2x+cos2x的值.
点评:本题考查二倍角的余弦,考查同角三角函数间的基本关系,求得sinx,cosx的值是关键,属于中档题.
 ,
,∴(sinx+cosx)2=
 ,
,即1+2sinxcosx=
 ,
,∴2sinxcosx=-
 ,
,∴(sinx-cosx)2=1-2sinxcosx=1+
 =
= ,
,又x∈(0,π),
∴sinx>0,cosx<0,
∴sinx-cosx>0,
sinx-cosx=
 ;
;(2)∵sinx+cosx=
 ,sinx-cosx=
,sinx-cosx= ;
;∴sinx=
 ,cosx=
,cosx= ,
,∴cos2x=cos2x-sin2x=
 -
- =-
=- ,
,∴sin2x+cos2x=-
 -
- =-
=-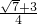 .
.分析:(1)依题意可知
 <x<π,从而可求得sinx-cosx的值;
<x<π,从而可求得sinx-cosx的值;(2)可求得sinx,cosx的值后,利用二倍角公式可求得sin2x,cos2x的值,继而可得sin2x+cos2x的值.
点评:本题考查二倍角的余弦,考查同角三角函数间的基本关系,求得sinx,cosx的值是关键,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知x∈(0,π],关于x的方程2sin(x+
)=a有两个不同的实数解,则实数a的取值范围为( )
| π |
| 3 |
A、[-
| ||
B、[
| ||
C、(
| ||
D、(
|