题目内容
6.已知直线y=kx-2k+1与圆(x-2)2+(y-1)2=3相交于M,N两点,则|MN|等于$2\sqrt{3}$.分析 根据已知可得直线恒过圆心,则|MN|即为直径.
解答 解:直线y=kx-2k+1恒过(2,1)点,
即直线y=kx-2k+1恒过圆(x-2)2+(y-1)2=3的圆心,
故|MN|=2R=$2\sqrt{3}$;
故答案为:$2\sqrt{3}$
点评 本题考查的知识点是直线与圆的位置关系,圆的弦长公式,难度中档.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
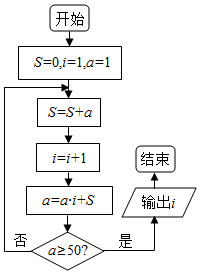
18.运行如图所示程序框图,输出的结果是( )


| A. | 15 | B. | 23 | C. | 47 | D. | 95 |
15.已知命题p:所有有理数都是实数;命题q:y=x2是奇函数.则下列命题中为真命题的是( )
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨(¬q) |
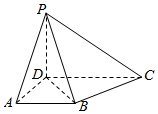 在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.