题目内容
已知-2≤a≤4，3≤b≤6，求ab的取值范围．
考点：不等关系与不等式
专题：不等式的解法及应用
分析：当0≤a≤4时，和当-2≤a＜0时分别由不等式的可乘性可得ab的范围，取并集综合可得．
解答：
解：当0≤a≤4时，由3≤b≤6可得0≤ab≤24；
当-2≤a＜0时，可得0＜-a≤2，
∴0＜-ab≤12，即-12≤ab＜0，
综合可得ab的取值范围为：[-12，24]
当-2≤a＜0时，可得0＜-a≤2，
∴0＜-ab≤12，即-12≤ab＜0，
综合可得ab的取值范围为：[-12，24]
点评：本题考查不等式的性质，涉及分类讨论的思想，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=
为R的单调函数，则实数a的取值范围是（ ）
|
| A、（0，+∞） |
| B、[-1，0） |
| C、（-2，0） |
| D、（-∞，-2） |
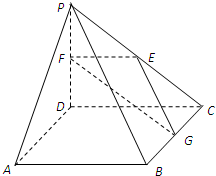如图，在四棱锥P-ABCD中，ABCD是正方形，PD⊥平面ABCD，PD=AB=2，E，F，G分别是PC，PD，BC的中点．
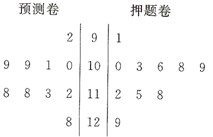安徽某所学校高三年级有10名同学参加2014年北约自主招生，学校对这10名同学进行了辅导，并进行了两次模拟考试，检测成绩的茎叶图如图所示．
已知|