题目内容
16.若直线$x+\sqrt{3}y=a$与圆x2+y2=1在第一象限有两个不同的交点,则实数a的取值范围是($\sqrt{3}$,2).分析 抓住两个关键点,一是直线过(0,1);一是直线与圆相切,分别求出m的值,即可确定出直线与圆在第一象限内有两个不同的交点时a的范围.
解答 解:分两种情况:当直线$x+\sqrt{3}y=a$过(0,1)时,将x=0,y=1代入得:a=$\sqrt{3}$;
当直线$x+\sqrt{3}y=a$与圆 x2+y2=1相切时,圆心到直线的距离d=$\frac{|a|}{\sqrt{1+3}}$=r=1,
x2+y2=1相切时,圆心到直线的距离d=$\frac{|a|}{\sqrt{1+3}}$=r=1,
解得:a=2或-2(舍去),
则直线与圆在第一象限内有两个不同的交点时,实数a的取值范围是($\sqrt{3}$,2).
故答案为($\sqrt{3}$,2).
点评 此题考查了直线与圆的位置关系,解题的关键是抓住两个关键点,一是直线过(0,1);一是直线与圆相切.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
6.若a=20.1,b=ln2,c=log0.36,则a,b,c的大小关系为( )
| A. | a>c>b | B. | c>b>a | C. | a>b>c | D. | b>c>a |
7.数列2,5,10,17,…的第n项an可能为( )
| A. | 2n | B. | n2+n | C. | 2n-1 | D. | n2+1 |
4.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据涪陵气象局某日早6点至晚9点在李渡新城区、涪陵老城区两个地区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,李渡新城区、涪陵老城区浓度的方差较小的是( )
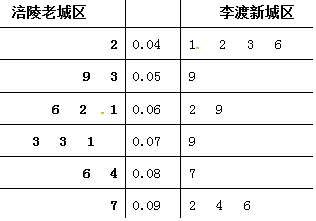

| A. | 李渡新城区 | B. | 涪陵老城区 | ||
| C. | 李渡新城区、涪陵老城区相等 | D. | 无法确定 |
1.若f(x)=-$\frac{1}{2}$(x-2)2+blnx在(1,+∞)上是减函数,则b的取值范围是( )
| A. | [-1,+∞) | B. | (-1,+∞) | C. | (-∞,-1] | D. | (-∞,-1) |
12.已知log23=a,log25=b,则${log_2}\frac{9}{5}$=( )
| A. | $\frac{2a}{b}$ | B. | 2a-b | C. | a2-b | D. | $\frac{a^2}{b}$ |