题目内容
8.若函数f(x)=21n(x+1)-1nax在其定义域内有且只有一个零点,则实数a的取值集合为( )| A. | |4| | B. | (-∞,4] | C. | (-∞,0) | D. | (-∞,0)∪{4} |
分析 化简可得(x+1)2=ax在(-1,+∞)上有且只有一个解,从而讨论解得即可.
解答 解:∵函数f(x)=21n(x+1)-1nax在其定义域内有且只有一个零点,
∴21n(x+1)=1nax有且只有一个解,
∴(x+1)2=ax在(-1,+∞)上有且只有一个解,
∵$\frac{1}{a}$=$\frac{x}{(x+1)^{2}}$=$\frac{1}{x+1}$-$\frac{1}{(x+1)^{2}}$=-($\frac{1}{x+1}$-$\frac{1}{2}$)2+$\frac{1}{4}$≤$\frac{1}{4}$,
∴a<0或a≥4,
①当a<0时,作函数y=21n(x+1)与y=1nax的图象如下,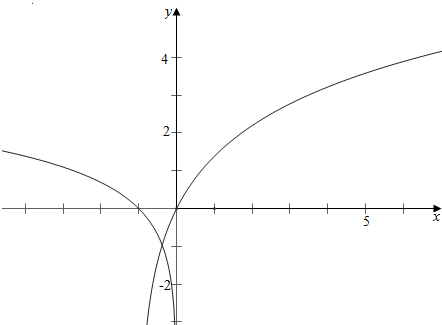
②当a=4时,(x+1)2=4x的解为x=1(成立),
③当a>4时,(x+1)2=ax可化为
x2-(a-2)x+1=0,
△=(a-2)2-4>0,
且a-2>0,1>0,
故(x+1)2=ax有两个不同的正根;
故实数a的取值集合为(-∞,0)∪{4},
故选:D.
点评 本题考查了函数的零点与方程的根的关系应用及分类讨论的应用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
18.已知变量x与y负相关,且由观测数据算得样本平均数$\overline{x}$=4,$\overline{y}$=2.5,则由该观测数据算得的线性回归方程可能是( )
| A. | $\widehat{y}$=0.4x+0.9 | B. | $\widehat{y}$=2x-5.5 | C. | $\widehat{y}$=-2x+10.5 | D. | $\widehat{y}$=-0.3x+4.7 |
19.“方程$\frac{{x}^{2}}{2+n}$-$\frac{{y}^{2}}{n+1}$=1表示双曲线”是“n>-1”的( )
| A. | 充分不必要条件 | B. | 必要且不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知a,b是两条不重合的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | 若a⊥b,a⊥α,则b∥α | B. | 若a⊥α,b∥α,则a⊥b | ||
| C. | 若a∥b,b?α,则a∥α | D. | 若a,b?α,a∥β,b∥β,则α∥β |
3.下列不等式一定成立的是( )
| A. | sinx+$\frac{1}{sinx}$≥2 | B. | x2+4≥4|x| | C. | lg(x2+1)>lg(2x) | D. | $\frac{1}{a}$+$\frac{1}{b}$>$\frac{2}{\sqrt{ab}}$ |
17.已知正项等比数列{an},其前n项和为Sn,ak-1=2,ak•ak+2=a${\;}_{5}^{2}$=64,则S10等于( )
| A. | 410-1 | B. | $\frac{{4}^{10}-1}{3}$ | C. | 210-1 | D. | $\frac{{2}^{10}-1}{2}$ |
18.幂函数的图象过点(5,$\sqrt{5}$),则它的单调递增区间是( )
| A. | [0,+∞) | B. | [-1,+∞) | C. | (-∞,+∞) | D. | (-∞,0) |