题目内容
18.若在定义域内存在实数x满足f(-x)=f(x),则称函数f(x)为“局部偶函数”.(Ⅰ)判断函数f(x)=x-$\frac{1}{x}$是否为“局部偶函数”,并说明理由;
(Ⅱ)若F(x)=$\left\{\begin{array}{l}{{9}^{x}-k•{3}^{x}+{k}^{2}-16,x>0}\\{k•{3}^{x}-{9}^{x},x<0}\end{array}\right.$为“局部偶函数”,求实数k的取值范围.
分析 (Ⅰ)若函数f(x)=x-$\frac{1}{x}$是“局部偶函数”,则f(-x)=f(x)有解,-x+$\frac{1}{x}$=x-$\frac{1}{x}$,求出x即可;
(Ⅱ)若F(x)=$\left\{\begin{array}{l}{{9}^{x}-k•{3}^{x}+{k}^{2}-16,x>0}\\{k•{3}^{x}-{9}^{x},x<0}\end{array}\right.$为“局部偶函数”,分类讨论,即可求实数k的取值范围.
解答 解:(Ⅰ)若函数f(x)=x-$\frac{1}{x}$是“局部偶函数”,则f(-x)=f(x)有解,
∴-x+$\frac{1}{x}$=x-$\frac{1}{x}$,
∴$\frac{1}{x}$=x,∴x=±1;
(Ⅱ)若F(x)=$\left\{\begin{array}{l}{{9}^{x}-k•{3}^{x}+{k}^{2}-16,x>0}\\{k•{3}^{x}-{9}^{x},x<0}\end{array}\right.$为“局部偶函数”,
则x>0,k•3-x-9-x=9x-k•3x+k2-16,
令t=3x+3-x(t>2),则t2-kt+k2-18=0有大于2的解,∴$\frac{k+\sqrt{72-3{k}^{2}}}{2}$>2,∴k>1-$\sqrt{15}$;
x<0,k•3x-9x=9-x-k•3-x+k2-16,
令t=3x+3-x(0<t<2),则t2-kt+k2-18=0有大于0,小于2的解,
∴$\left\{\begin{array}{l}{{k}^{2}-18>0}\\{4-2k+{k}^{2}-18<0}\end{array}\right.$或$\left\{\begin{array}{l}{{k}^{2}-4({k}^{2}-18)≥0}\\{0<\frac{k}{2}<2}\\{{k}^{2}-18>0}\\{4-2k+{k}^{2}-18>0}\end{array}\right.$,∴3$\sqrt{2}$<k<1+$\sqrt{15}$,
综上所述,k>1-$\sqrt{15}$或3$\sqrt{2}$<k<1+$\sqrt{15}$.
点评 本题考查局部偶函数,考查学生的计算能力,考查分类讨论的数学思想,属于中档题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | (2,-4,2) | B. | (-2,4,-2) | C. | (-2,0,-2) | D. | (2,1,-3) |
| A. | ($\frac{1}{2}$,2) | B. | (-∞,$\frac{1}{2}$)∪(2,+∞) | C. | ($\frac{1}{2}$,1)∪(2,+∞) | D. | (0,2) |
| A. | 2 | B. | 1 | C. | $\frac{17}{4}$ | D. | $\frac{15}{4}$ |
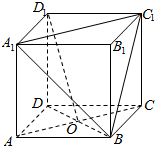 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.