Question

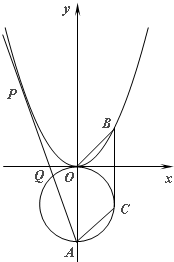
如图，已知x²+（y+2）²=4与坐标轴相交于O、A两点（O为坐标原点），另有抛物线y=ax²（a＞0）．
（Ⅰ）若抛物线上存在点B，直线BC切园于点C，四边形OACB是平行四边形，求抛物线的方程；
（Ⅱ）过点A作抛物线的切线，切点为P，直线AP与园相交于另一点Q，求

|AQ|

|QP|

的取值范围．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）先确定C，B的坐标，再求出a，即可求抛物线的方程；
（Ⅱ）求出AP的方程，代入A的坐标，再与圆的方程联立，求出Q的坐标，即可求

|AQ|

|QP|

的取值范围．

解答： 解：（Ⅰ）∵OACB是平行四边形，OA∥BC，
∴C（2，-2），B（2，4a），
又A（0，-4），∴4a-4=-2，解得a=

1

2

．
∴抛物线的方程为y=

1

2

x²．
（Ⅱ）不妨设P（t，at²）（t≠0）．
∵y'|_x=t=2ax|_x=t=2at，
∴AP的方程为y=2at（x-t）+at²，即y=2atx-at²．
又A（0，-4），∴at²=4，即a=

4

t2

．
∴AP的方程为y=

8

t

x-4．
联立方程组

y= 8 t x-4 x2+(y+2)2=4

，消去y，得（t²+64）x²-32tx=0．
∴Q的横坐标为xQ=

32t

t2+64

．
∴

|AQ|

|QP|

=

xQ-xA

xP-xQ

=

32

t2+32

．
又t2=

4

a

∈(0，+∞)，∴

|AQ|

|QP|

的取值范围是（0，1）．

点评：本题考查抛物线方程，考查直线与圆的位置关系，考查导数知识的运用，考查学生的计算能力，属于中档题．