题目内容
已知c是实数,二次方程x2+x+c=0有两个复数根a,b.若|a-b|=3,则c=( )
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
考点:复数求模
专题:数系的扩充和复数
分析:利用一元二次方程的根与系数的关系即可得出.
解答:
解:∵二次方程x2+x+c=0有两个复数根a,b.
∴a+b=-1,ab=c.
∵|a-b|=3,
∴3=
,
∴3=
,
解得c=-2.
故选:C.
∴a+b=-1,ab=c.
∵|a-b|=3,
∴3=
| (a+b)2-4ab |
∴3=
| 1-4c |
解得c=-2.
故选:C.
点评:本题考查了一元二次方程的根与系数的关系,属于基础题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
曲线y=x3-3x2+1在x=1处的切线方程为( )
| A、y=3x-4 |
| B、y=-3x+2 |
| C、y=-3x+3 |
| D、y=4x-5 |
已知{an}为等差数列,a2+a3+a4=30,a5+a6=40,则公差d等于( )
| A、2 | B、2 | C、4 | D、5 |
下列四个关系中,正确的是( )
| A、a∈{a,b} |
| B、{a}∈{a,b} |
| C、a∉{a} |
| D、a∉{a,b} |
已知函数f(x)=3x3+2x,则f(2)=( )
| A、10 | B、28 | C、31 | D、18 |
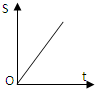
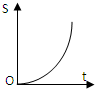
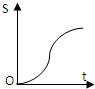
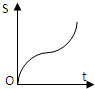
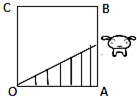 如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )
如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )