题目内容
在Rt△ABC中，∠C=90°，AC=4，则
•
=（ ）
| AB |
| AC |
| A、-16 | B、16 | C、-9 | D、9 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量垂直与数量积的关系、向量的三角形法则即可得出．
解答：
解：∵∠C=90°，
∴
•
=0．
∴
•
=(
-
)•
=
2=16．
故选：B．
∴
| CB |
| AC |
∴
| AB |
| AC |
| CB |
| CA |
| AC |
| AC |
故选：B．
点评：本题考查了向量垂直与数量积的关系、向量的三角形法则，属于基础题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
若定义在R上的偶函数f（x）满足f（x+2）=f（x）且x∈[0，1]时，f（x）=x，则方程f（x）=log3|x|的零点个数是（ ）
| A、2个 | B、3个 | C、4个 | D、6个 |
已知圆锥曲线x2+my2=1的一个焦点坐标为F（
，0），则该圆锥曲线的离心率为（ ）
| 2 | ||
|
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
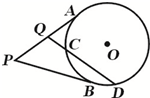已知PA，PB分别为⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC=2，CD=3，则PB=