题目内容
9.已知角α=$\frac{5π}{6}$,则,其终边与单位圆交点的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).分析 根据任意角的三角函数的定义即可求出.
解答 解:由于角α=$\frac{5π}{6}$的终边与单位圆的交点的横坐标是cos$\frac{5π}{6}$=-$\frac{\sqrt{3}}{2}$,
由于角α=$\frac{5π}{6}$的终边与单位圆的交点的纵坐标是sin$\frac{5π}{6}$=$\frac{1}{2}$,
∴角的终边与单位圆的交点的坐标是(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
故答案为:(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
14.已知两个不共线的向量$\overrightarrow{OA}$和$\overrightarrow{OC}$,向量$\overrightarrow{OB}$与$\overrightarrow{OA}$关于向量$\overrightarrow{OC}$对称,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{b}$用$\overrightarrow{a}$和$\overrightarrow{c}$表示为( )
| A. | 2($\overrightarrow{a}$•$\overrightarrow{c}$)$\overrightarrow{c}$-$\overrightarrow{a}$ | B. | $\frac{2(\overrightarrow{a}•\overrightarrow{c})}{|\overrightarrow{c}|}•\overrightarrow{c}-\overrightarrow{a}$ | C. | $\frac{2(\overrightarrow{a}•\overrightarrow{c})}{|\overrightarrow{c}|}-\overrightarrow{a}$ | D. | $\frac{2(\overrightarrow{a}•\overrightarrow{c})}{|\overrightarrow{c}{|}^{2}}•\overrightarrow{c}-\overrightarrow{a}$ |
20.已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
| A. | ?x0∈R,f(x0)=0 | |
| B. | 若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 若x0是f(x)的极值点,则f′(x0)=0 |
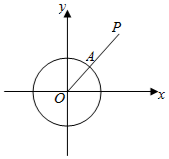 在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).
在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).