题目内容
8.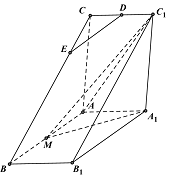 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.(1)若BE=3EC,求证:DE∥平面A1MC1;
(2)若AA1=l,求三棱锥A-MA1C1的体积.
分析 (1)取BC中点为N,连结MN,C1N,则MN∥AC∥A1C1,从而DE∥NC1.由此能证明DE∥平面A1MC1.
(2)三棱锥A-MA1C1的体积${V_{A-{A_1}M{C_1}}}={V_{{C_1}-{A_1}AM}}$.由此能求出结果.
解答 证明:(1)如图1,取BC中点为N,连结MN,C1N,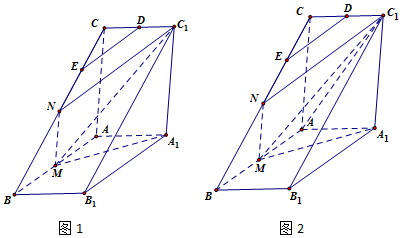
∵M是AB中点,∴MN∥AC∥A1C1,
∴M,N,C1,A1共面.
∵BE=3EC,∴E是NC的中点.
又D是CC1的中点,∴DE∥NC1.
∵DE?平面MNC1A1,NC1?平面MNC1A1,
∴DE∥平面A1MC1.
解:(2)如图2,当AA1=1时,
则AM=1,A1M=$\sqrt{2}$,A1C1=$\sqrt{2}$.
∴三棱锥A-MA1C1的体积:
${V_{A-{A_1}M{C_1}}}={V_{{C_1}-{A_1}AM}}=\frac{1}{3}•\frac{1}{2}AM•A{A_1}•{A_1}{C_1}=\frac{{\sqrt{2}}}{6}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
20.已知$\overrightarrow{e_1},\overrightarrow{e_2}$是夹角为60°的两个单位向量,则“实数k=4”是“$(2\overrightarrow{e_1}-k\overrightarrow{e_2})⊥\overrightarrow{e_1}$”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
17.已知$a={2^{-\frac{1}{3}}}$,$b={({2^{{{log}_2}3}})^{-\frac{1}{2}}}$,$c=\frac{1}{4}\int_0^π{sinxdx}$,则实数a,b,c的大小关系是( )
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | c>b>a |
18.已知$f(x)=\frac{{{x^2}+33}}{x}(x∈{N^*})$,则f(x)在定义域上的最小值为( )
| A. | $\frac{58}{5}$ | B. | $\frac{23}{2}$ | C. | $\sqrt{33}$ | D. | $2\sqrt{33}$ |