题目内容
在平面直角坐标系xOy中，设M是椭圆
+
=1（a＞b＞0）上在第一象限的点，A（a，0）和B（0，b）是椭圆的两个顶点，求四边形MAOB的面积的最大值．
| x2 |
| a2 |
| y2 |
| b2 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：令M（acosφ，bsinφ），其中0＜φ＜
，表示出四边形MAOB的面积，利用三角函数的有界限求出四边形OAMB的面积的最大值．
| π |
| 2 |
解答：
解：已知椭圆
+
=1的参数方程为
．
由题设可令M（acosφ，bsinφ），其中0＜φ＜
．
所以，S四边形MAOB=S△MAO+S△MOB=
OA•yM+
OB•xM=
ab（sinφ+cosφ）=
absin（φ+
）．
所以，当φ=
时，四边形MAOB的面积的最大值为
ab．
| x2 |
| a2 |
| y2 |
| b2 |
|
由题设可令M（acosφ，bsinφ），其中0＜φ＜
| π |
| 2 |
所以，S四边形MAOB=S△MAO+S△MOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
所以，当φ=
| π |
| 4 |
| ||
| 2 |
点评：本题考查椭圆上的点的设法及三角函数的有界限求函数的最值，属于一道中档题．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
如图，直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形，AB∥CD，∠BAD=90°，P是棱CD上一点，AB=2，AD=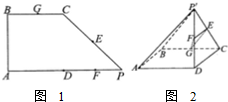
如图1所示，在直角梯形ABCP中，AP∥BC，AP⊥AB，AP=2AB=2BC，D是底边AP的中点，E．F、G分别为PC、PD、CB的中点，将△PCD沿CD折起，使点P位于点P′，且P′D⊥平面ABCD，得折叠后如图2的几何图形．
如图，已知底面圆半径为4的圆锥SO中，S为顶点，O为底面圆心，SB、SC是母线，∠BOC=120°，作OA⊥SC于A点，若将△SAO绕轴旋转一周所得几何体的体积是圆锥SO体积的
在长方体ABCD-A1B1C1D1中，已知AB=4，BC=3，CC1=5，求：