题目内容

1．求证：tan（x-y）+tan（y-z）+tan（z-x）=tan（x-y）tan（y-z）tan（z-x）．

分析 由tan（x-z）=tan[（x-y）+（y-z）]，展开两角差的正切后移项变形得答案．

解答 证明：∵tan（x-z）=tan[（x-y）+（y-z）]=$\frac{tan（x-y）+tan（y-z）}{1-tan（x-y）tan（y-z）}$，
∴tan（x-z）-tan（x-z）tan（x-y）tan（y-z）=tan（x-y）+tan（y-z），
∴tan（x-y）+tan（y-z）+tan（z-x）=tan（x-y）tan（y-z）tan（z-x）．

点评 本题考查三角恒等式的证明，考查了两角差的正切，是中档题．

练习册系列答案
相关题目
11．下列四种说法：
①在一个算法的程序框图中有时可以不用条件结构；
②在一个算法的程序框图中有时可以不用循环结构；
③在一个算法的程序框图中一定要用顺序结构；
④在一个算法的程序框图中条件结构与循环结构至少要用一个，
其中说法正确的个数是（　　）
A．1B．2C．3D．4
12．已知函数f（x）=2sin（2x+$\frac{π}{3}$），其中x∈R，给出下列结论：①将y=2sin2x的图象向左平移$\frac{π}{6}$个单位长度可得到函数f（x）的图象；②f（x）是最小正周期为π的偶函数：③f（x）的一条对称轴是x=$\frac{π}{3}$；④f（x）的一个对称中心为（$\frac{π}{12}$，0）．其中正确的结论是①（只填序号）．
9．复数z满足z2+2z=-10，则|z|=$\sqrt{10}$．
16．设椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左，右焦点分别为F1，F2，上顶点为点A，点B，F2关于F1对称，抛物线y2=4x的准线经过F1交AB于P，且$\frac{B{F}_{1}}{AB}$=$\frac{P{F}_{1}}{A{F}_{2}}$．
（1）求椭圆E的方程；
（2）已知定点Q（t，0）（t＞0），若斜率为1的直线1过点Q与椭圆E交于不同的两点C，D，且对椭圆E上任意一点N，都存在θ∈[0，2π]，使得$\overrightarrow{ON}$=cosθ$•\overrightarrow{OC}$+sinθ$•\overrightarrow{OD}$成立，求满足条件的实数t的值．
6．计算：
（1）sin$\frac{π}{12}$cos$\frac{π}{12}$=$\frac{1}{4}$；
（2）cos105°cos15°=$-\frac{1}{4}$；
（3）sin2$\frac{π}{12}$-cos2$\frac{π}{12}$=$-\frac{\sqrt{3}}{2}$；
（4）$\frac{tan67.5°}{1-ta{n}^{2}67.5°}$=$-\frac{1}{2}$．
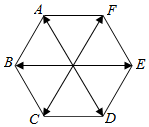13．如图，在正六边形ABCDEF中，与$\overrightarrow{OA}$-$\overrightarrow{OC}$+$\overrightarrow{CD}$相等的向量有①．（填序号）
①$\overrightarrow{CF}$；②$\overrightarrow{AD}$；③$\overrightarrow{DA}$；④$\overrightarrow{BE}$；⑤$\overrightarrow{CE}$+$\overrightarrow{BC}$；⑥$\overrightarrow{CA}$-$\overrightarrow{CD}$；⑦$\overrightarrow{AB}$+$\overrightarrow{AE}$．
10．若函数f（x）是周期为6的奇函数，且f（1）=1，则f（2015）=-1．
11．若{an}是公差为1的等差数列，则{a2n-1+2a2n}的公差为6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网