题目内容
12.已知函数f(x)=2sin(2x+$\frac{π}{3}$),其中x∈R,给出下列结论:①将y=2sin2x的图象向左平移$\frac{π}{6}$个单位长度可得到函数f(x)的图象;②f(x)是最小正周期为π的偶函数:③f(x)的一条对称轴是x=$\frac{π}{3}$;④f(x)的一个对称中心为($\frac{π}{12}$,0).其中正确的结论是①(只填序号).分析 由条件利用正弦函数的图象和性质,y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:对于函数f(x)=2sin(2x+$\frac{π}{3}$),其中x∈R,
①将y=2sin2x的图象向左平移$\frac{π}{6}$个单位长度可得到函数y=2sin2(x+$\frac{π}{6}$)=2sin(2x+$\frac{π}{3}$)=f(x)的图象,
故①正确;
②f(x)是最小正周期为$\frac{2π}{2}$=π的非奇非偶函数,故②错误;
③当x=$\frac{π}{3}$时,求得f(x)=0,不是最值,可得f(x)的图象不关于直线x=$\frac{π}{3}$对称,故③错误;
④令x=$\frac{π}{12}$,求得f(x)=2,为函数的最大值,故f(x)的一条对称轴为x=$\frac{π}{12}$,故④错误,
故答案为:①.
点评 本题主要考查正弦函数的图象和性质,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
3.记Sn为正项等比数列{an}的前n项和,若$\frac{{S}_{12}-{S}_{6}}{{S}_{6}}$-7•$\frac{{S}_{6}-{S}_{3}}{{S}_{3}}$-8=0,且正整数m,n满足a1ama2n=2${a}_{5}^{3}$,则$\frac{1}{m}$+$\frac{8}{n}$的最小值是( )
| A. | $\frac{7}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{9}{5}$ | D. | $\frac{15}{7}$ |
7.下列三个图中的多边形均为正多边形,A(B)是正多边形的顶点,椭圆过A(B)且均以图中的F1,F2为焦点,设图①,②,③中的椭圆的离心率分别为e1,e2,e3,则( )


| A. | e1>e2>e3 | B. | e3>e1>e2 | C. | e1<e3<e2 | D. | e1<e2<e3 |
2.在△ABC中,若tanB=$\frac{cos(C-B)}{sinA+sin(C-B)}$,则这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形 | D. | 等腰三角形或直角三角形 |
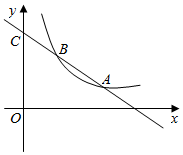 如图函数y1=k1x+b的图象与函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象交于A、B两点,与y轴交于c点.已知A点的坐标为(2,1).c点坐标为(0.3).
如图函数y1=k1x+b的图象与函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象交于A、B两点,与y轴交于c点.已知A点的坐标为(2,1).c点坐标为(0.3).