题目内容
设函数f(x)=
x3+
x2+bx+1.
(Ⅰ)(ⅰ)若b=2时,f(x)在R上单调递增,求实数a的取值范围;
(ⅱ)若对任意a∈[1,+∞),存在x∈(2,3),使得f(x)>0,求实数b的取值范围;
(Ⅱ)已知函数f(x)有两个不同的极值点x1,x2(x1<x2),存在实数n,有n<x1<x2<n+1,f′(x)为f(x)的导函数.求证:max{min{f′(n),f′(n+1)},
}=
.(其中min{a,b}指a,b中的最小值,max{a,b}指a,b中的最大值).
| 1 |
| 3 |
| a |
| 2 |
(Ⅰ)(ⅰ)若b=2时,f(x)在R上单调递增,求实数a的取值范围;
(ⅱ)若对任意a∈[1,+∞),存在x∈(2,3),使得f(x)>0,求实数b的取值范围;
(Ⅱ)已知函数f(x)有两个不同的极值点x1,x2(x1<x2),存在实数n,有n<x1<x2<n+1,f′(x)为f(x)的导函数.求证:max{min{f′(n),f′(n+1)},
| 1 |
| 4 |
| 1 |
| 4 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)(ⅰ)f(x)在R上单调递增,f′(x)=x2+ax+2≥0恒成立,则△=a2-8≤0,即可求实数a的取值范围;
(ⅱ)存在x∈(2,3),-b<
=
x+
+
x2,h(x)=
x+
+
x2,x∈(2,3),h(x)在(2,3)递增,h(3)=
,即可求实数b的取值范围;
(Ⅱ)证明
≤n+
时,min{f′(n),f′(n+1)}=f′(n)=f′(n)<
,
>n+
时,min{f′(n),f′(n+1)}=f′(n)=f′(n+1)<
,即可得出结论.
(ⅱ)存在x∈(2,3),-b<
| ||||
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 29 |
| 6 |
(Ⅱ)证明
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
(Ⅰ)(ⅰ)解:b=2时,f′(x)=x2+ax+2≥0恒成立,
∴△=a2-8≤0,
∴-2
≤a≤2
;
(ⅱ)解:令g(a)=
x3+
x2+bx+1,
∵a≥1,
∴g(a)min=g(1)=
x3+
x2+bx+1,
∵存在x∈(2,3),使得f(x)>0,
∴存在x∈(2,3),-b<
=
x+
+
x2,
令h(x)=
x+
+
x2,x∈(2,3),
∴h'(x)=
-
+
x=
+
x>0,
∴h(x)在(2,3)递增,h(3)=
,
∴-b<
即b>
,
(Ⅱ)证明:f′(x)=x2+ax+b=(x-x1)(x-x2),对称轴为x=
,
≤n+
时,min{f′(n),f′(n+1)}=f′(n)=f′(n),
f′(n)=(n-x1)(n-x2),
-
≤n-x1<0,
≤n-x2<0,
∴0<(n-x1)(n-x2)≤
-(
)2<
,
∴min{f′(n),f′(n+1)}=f′(n)=f′(n)<
,
>n+
时,min{f′(n),f′(n+1)}=f′(n)=f′(n+1),
f′(n+1)=(n+1-x1)(n+1-x2),0<n+1-x1<
+
,0<n+1-x2<
+
,
∴0<(n+1-x1)(n+1-x2)≤
-(
)2<
,
∴min{f′(n),f′(n+1)}=f′(n)=f′(n+1)<
,
∴max{min{f′(n),f′(n+1)},
}=
.
∴△=a2-8≤0,
∴-2
| 2 |
| 2 |
(ⅱ)解:令g(a)=
| 1 |
| 3 |
| a |
| 2 |
∵a≥1,
∴g(a)min=g(1)=
| 1 |
| 3 |
| 1 |
| 2 |
∵存在x∈(2,3),使得f(x)>0,
∴存在x∈(2,3),-b<
| ||||
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
令h(x)=
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
∴h'(x)=
| 1 |
| 2 |
| 1 |
| x2 |
| 2 |
| 3 |
| x2-2 |
| 2x2 |
| 2 |
| 3 |
∴h(x)在(2,3)递增,h(3)=
| 29 |
| 6 |
∴-b<
| 29 |
| 6 |
| 29 |
| 6 |
(Ⅱ)证明:f′(x)=x2+ax+b=(x-x1)(x-x2),对称轴为x=
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
f′(n)=(n-x1)(n-x2),
| x2-x1 |
| 2 |
| 1 |
| 2 |
| x1-x2 |
| 2 |
| 1 |
| 2 |
∴0<(n-x1)(n-x2)≤
| 1 |
| 4 |
| x1-x2 |
| 2 |
| 1 |
| 4 |
∴min{f′(n),f′(n+1)}=f′(n)=f′(n)<
| 1 |
| 4 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
f′(n+1)=(n+1-x1)(n+1-x2),0<n+1-x1<
| x2-x1 |
| 2 |
| 1 |
| 2 |
| x1-x2 |
| 2 |
| 1 |
| 2 |
∴0<(n+1-x1)(n+1-x2)≤
| 1 |
| 4 |
| x1-x2 |
| 2 |
| 1 |
| 4 |
∴min{f′(n),f′(n+1)}=f′(n)=f′(n+1)<
| 1 |
| 4 |
∴max{min{f′(n),f′(n+1)},
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查导数知识的综合运用,考查函数的单调性,考查学生分析解决问题的能力,有难度.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
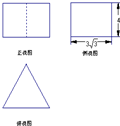 已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.
已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.