题目内容
某个年级有男生560人，女生420人，用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，则此样本中男生人数为（ ）
| A、120 | B、160 |
| C、140 | D、100 |
考点：分层抽样方法
专题：概率与统计
分析：先根据男生和女生的人数做出年纪大总人数，用要抽取得人数除以总人数得到每个个体被抽到的概率，用男生人数乘以概率，得到结果．
解答：
解：∵有男生560人，女生420人，
∴年级共有560+420=980，
∵用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，
∴每个个体被抽到的概率是
=
，
∴要从男生中抽取560×
=160，
故选：B．
∴年级共有560+420=980，
∵用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，
∴每个个体被抽到的概率是
| 280 |
| 980 |
| 2 |
| 7 |
∴要从男生中抽取560×
| 2 |
| 7 |
故选：B．
点评：本题考查分层抽样方法，本题解题的关键是在抽样过程中每个个体被抽到的概率相等，这是解题的依据，本题是一个基础题．
练习册系列答案
相关题目
下列各角中与角-
终边相同的是（ ）
| π |
| 3 |
| A、300° | ||
| B、240° | ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）上的点（2，1）到该点较近的渐近线的距离为
（其中e为离心率），则双曲线的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| e |
A、
| ||||
B、
| ||||
| C、x2-3y2=1 | ||||
D、
|
已知集合A={x|3x+x2＞0}，B={x|-4＜x＜-1}，则（ ）
| A、A∩B={x|-4＜x＜-3} |
| B、A∪B=R |
| C、B⊆A |
| D、A⊆B |
若集合A={x|x≥1}，且A∩B=B，则集合B可能是（ ）
| A、{1，2} |
| B、{x|x≤1} |
| C、{-1，0，1} |
| D、R |
函数f（x）=
的定义域为（ ）
| 1 | ||||
|
| A、（2，+∞） | ||
| B、（0，2） | ||
| C、（-∞，2） | ||
D、（0，
|
已知函数f（x）=x（lnx-
ax）有两个极值点，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、（-∞，0） | ||
B、（0，
| ||
| C、（0，1） | ||
| D、（0，+∞） |
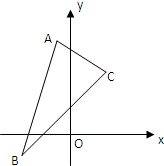已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）．