题目内容
已知集合A={x|3x+x2＞0}，B={x|-4＜x＜-1}，则（ ）
| A、A∩B={x|-4＜x＜-3} |
| B、A∪B=R |
| C、B⊆A |
| D、A⊆B |
考点：交集及其运算,并集及其运算
专题：集合
分析：求出A中不等式的解集确定出A，找出A与B的交集、并集，判断出A与B的包含关系即可．
解答：
解：由A中不等式变形得：x（x+3）＞0，
解得：x＜-3或x＞0，即A={x|x＞0或x＜-3}，
∵B={x|-4＜x＜-1}，
∴A∩B={x|-4＜x＜-3}，A∪B={x|x＞0或x＜-1}．
故选：A．
解得：x＜-3或x＞0，即A={x|x＞0或x＜-3}，
∵B={x|-4＜x＜-1}，
∴A∩B={x|-4＜x＜-3}，A∪B={x|x＞0或x＜-1}．
故选：A．
点评：此题考查了交集及其运算，并集及其运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
若复数z满足
=4-3i，则|z|等于（ ）
| (1-2i)2 |
| z |
| A、1 | ||
B、
| ||
| C、5 | ||
D、
|
已知集合A={-1，1，2}，集合B={1，3，5}，则A∩B=（ ）
| A、{-1，1，2，3，5} | B、{1} |
| C、∅ | D、{∅} |
用数学归纳法证明“5n-2n能被3整除”的第二步中，n=k+1时，为了使用假设，应将5k+1-2k+1变形为（ ）
| A、5（5k-2k）+3×2k |
| B、（5k-2k）+4×5k-2k |
| C、（5-2）（5k-2k） |
| D、2（5k-2k）-3×5k |
“所有9的倍数都是3的倍数，369是9的倍数，故369是3的倍数”，上述推理（ ）
| A、小前提错 | B、结论错 |
| C、大前提错 | D、正确 |
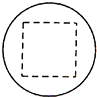已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是（ ）| A、64π | B、32π |
| C、16π | D、12π |
某个年级有男生560人，女生420人，用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，则此样本中男生人数为（ ）
| A、120 | B、160 |
| C、140 | D、100 |
若{1，2}⊆A⊆{1，2，3，4，5}，则集合A的个数是（ ）
| A、8 | B、7 | C、4 | D、3 |