题目内容
16.已知函数f(x)是定义在(-2,2)上的奇函数,且在[0,2)上为减函数,使 f(m)+f(2m-1)>0.求实数m的取值范围.分析 根据函数f(x)是奇函数,将不等式f(m)+f(2m-1)>0移项,整理得f(m)>f(1-2m).因为函数是定义在(-2,2)上的减函数,所以有-2<m<1-2m<2,解之即得实数m的取值范围.
解答 解:∵f(m)+f(2m-1)>0
∴移项,得f(m)>-f(2m-1)
又∵f(x)在(-2,2)上为奇函数
∴-f(2m-1)=f(1-2m)
且-2<2m-1<2…①,
∴f(m)>f(1-2m)
又∵f(x)在[0,2)上为减函数,
∴f(x)是定义在(-2,2)上的减函数
∴m<1-2m且-2<m<2…②,
联解①②,得-$\frac{1}{2}$<m<$\frac{1}{3}$,∴实数m的取值范围为(-$\frac{1}{2}$,$\frac{1}{3}$).
点评 本题给出一个定义在(-2,2)上的抽象函数,在已知其单调性和奇偶性的情况下,解关于m的不等式,着重考查了函数奇偶性与单调性的综合应用,属于基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
8.若角α是第三象限角,则cosα•$\sqrt{1+ta{n}^{2}α}$+$\frac{tanα}{\sqrt{\frac{1}{co{s}^{2}α}-1}}$的值为( )
| A. | 1 | B. | ±1 | C. | -1 | D. | 0 |
11.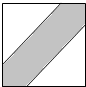 如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
 如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )| A. | $\frac{529}{625}$ | B. | $\frac{96}{625}$ | C. | $\frac{23}{25}$ | D. | $\frac{2}{25}$ |