题目内容
4.求$\frac{\sqrt{1+cos20°}}{2\sqrt{2}sin10°}$-sin10°•(cot5°-tan5°)的值.分析 利用切化弦以及二倍角公式以及和差化积公式化简求解即可.
解答 解:$\frac{\sqrt{1+cos20°}}{2\sqrt{2}sin10°}$-sin10°•(cot5°-tan5°)
=$\frac{\sqrt{2{cos}^{2}10°}}{2\sqrt{2}sin10°}$-sin10°•$\frac{{cos}^{2}5°-{sin}^{2}5°}{sin5°cos5°}$
=$\frac{cos10°}{2sin10°}$-$\frac{2sin10°cos10°}{sin10°}$
=$\frac{cos10°}{2sin10°}-2cos10°$
=$\frac{1}{2}$cot10°-2cos10°
=$\frac{cos10°-4cos10°sin10°}{2sin10°}$
=$\frac{sin80°-2sin20°}{2sin10°}$
=$\frac{2cos50°sin30°-sin20°}{2sin10°}$
=$\frac{sin40°-sin20°}{2sin10°}$
=$\frac{2cos30°sin10°}{2sin10°}$
=cos30°
=$\frac{\sqrt{3}}{2}$.
点评 本题主要考查利用同角三角函数的基本关系,和差化积公式的应用,利用二倍角的正弦、余弦公式进行化简求值,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
12.化简$\frac{1+sinα+cosα+2sinαcosα}{1+sinα+cosα}$的结果是( )
| A. | 2sinα | B. | 2cosα | C. | sinα-cosα | D. | sinα+cosα |
19.随着科技的进步,微爆技术正逐步被应用到我们日常生活中的各个方面,某医院为探究微爆技术在治疗肾结石方面的应用,设计了一个试验:在一个棱长为1cm的正方体的中心放置微量手术专用炸药,而爆炸的威力范围是一个半径为R的球,则爆炸之后形成的碎片全部落在正方体内部的概率为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{5}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{9}$ |
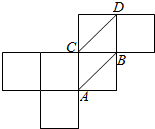 如图是一个正方体的展开图,在原正方体中直线AB与CD的位置关系是异面.
如图是一个正方体的展开图,在原正方体中直线AB与CD的位置关系是异面.