题目内容
5.已知向量$\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(2,1),$\overrightarrow{c}$=(3,-1),t∈R.(1)向量$\overrightarrow{a}$-$\overrightarrow{b}$会与非零向量t$\overrightarrow{c}$共线吗?
(2)t为何值时,$\overrightarrow{a}$-t$\overrightarrow{b}$与$\overrightarrow{c}$共线.
分析 (1)由已知向量的坐标求出$\overrightarrow{a}$-$\overrightarrow{b}$、t$\overrightarrow{c}$的坐标,结合向量共线的坐标表示可得向量$\overrightarrow{a}$-$\overrightarrow{b}$与非零向量t$\overrightarrow{c}$不共线;
(2)求出$\overrightarrow{a}$-t$\overrightarrow{b}$得坐标,由向量共线的坐标表示列式求得t的值.
解答 解:(1)∵$\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(2,1),
∴$\overrightarrow{a}$-$\overrightarrow{b}$=(-5,1),
又非零向量t$\overrightarrow{c}$=(3t,-t),
而-5(-t)-3t=2t≠0.
∴向量$\overrightarrow{a}$-$\overrightarrow{b}$与非零向量t$\overrightarrow{c}$不共线;
(2)$\overrightarrow{a}$-t$\overrightarrow{b}$=(-3-2t,2-t),$\overrightarrow{c}$=(3,-1),
由(-3-2t)(-1)-3(2-t)=0,解得:t=$\frac{3}{5}$.
∴当t=$\frac{3}{5}$时,$\overrightarrow{a}$-t$\overrightarrow{b}$与$\overrightarrow{c}$共线.
点评 平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若$\overrightarrow{a}$=(a1,a2),$\overrightarrow{b}$=(b1,b2),则$\overrightarrow{a}$⊥$\overrightarrow{b}$?a1a2+b1b2=0,$\overrightarrow{a}$∥$\overrightarrow{b}$?a1b2-a2b1=0,是基础题.

 名校课堂系列答案
名校课堂系列答案| A. | |3m-4n-5|=10 | B. | |3m-4n+5|=10 | C. | 3m-4n-5=10 | D. | 3m-4n+5=10 |
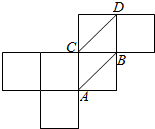 如图是一个正方体的展开图,在原正方体中直线AB与CD的位置关系是异面.
如图是一个正方体的展开图,在原正方体中直线AB与CD的位置关系是异面.