题目内容
6.在等差数列{an}中,a2=14,a5=5,则公差d=( )| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
分析 利用等差数列的通项公式及其性质即可得出.
解答 解:公差d=$\frac{{a}_{5}-{a}_{2}}{3}$=$\frac{5-14}{3}$=-3.
故选:B.
点评 本题考查了等差数列的通项公式及其性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.设某中学的高中女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,3,…,n),用最小二乘法近似得到回归直线方程为$\hat y=0.85x-85.71$,则下列结论中不正确的是( )
| A. | y与x具有正线性相关关系 | |
| B. | 回归直线过样本的中心点$(\overline x,\overline y)$ | |
| C. | 若该中学某高中女生身高增加1cm,则其体重约增加0.85kg | |
| D. | 若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg |
19.若复数$z=\frac{-2+3i}{i},i$是虚数单位,则z的共轭复数$\overline z$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.已知x,y取值如表:
画散点图分析可知:y与x线性相关,且求得回归方程为$\stackrel{∧}{y}$=x+1,则m的值为$\frac{3}{2}$.
| x | 0 | 1 | 3 | 5 | 6 |
| y | 1 | m | 3m | 5.6 | 7.4 |
17.已知函数f(x)=$\frac{{x}^{2}}{{e}^{x}}$,x≠0,e为自然对数的底数,关于x的方程$\sqrt{f(x)}$+$\frac{2}{\sqrt{f(x)}}$-λ=0有四个相异实根,则实数λ的取值范围是( )
| A. | (0,$\frac{2}{e}$) | B. | (2$\sqrt{2}$,+∞) | C. | (e+$\frac{2}{e}$,+∞) | D. | ($\frac{{e}^{2}}{2}$+$\frac{4}{{e}^{2}}$,+∞) |
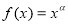 的图象经过点(2,4),则
的图象经过点(2,4),则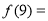 ( )
( ) 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 ( )
( ) ,存在
,存在 ,使
,使 成立,则
成立,则 ( )
( ) B.
B.
 D.
D.