��Ŀ����
ij��ҵ����20�������ߣ����������������ͼ���ˮƽ�����ص�Ӱ�죬�����һ�����Ĵ�Ʒ.���ݾ���֪����ÿ̨���������Ĵ�Ʒ�� �����ÿ̨�������ղ���
�����ÿ̨�������ղ��� ���
��� ֮�������ϵ��
֮�������ϵ��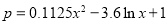 .��֪ÿ����1����ϸ�IJ�Ʒ������ӯ��3��Ԫ����ÿ����1�����Ʒ������1��Ԫ.
.��֪ÿ����1����ϸ�IJ�Ʒ������ӯ��3��Ԫ����ÿ����1�����Ʒ������1��Ԫ.
�����Խ�����ҵÿ���������ֲ�Ʒ����õ����� ��ʾΪ
��ʾΪ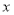 �ĺ�����
�����
����ÿ̨�������ղ���Ϊ����ʱ������ҵ������������Ϊ���٣�
��ϰ��ϵ�д�
�����Ŀ
19��������$z=\frac{-2+3i}{i}��i$��������λ����z�Ĺ����$\overline z$�ڸ�ƽ���ڶ�Ӧ�ĵ��ڣ�������
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
17����֪����f��x��=$\frac{{x}^{2}}{{e}^{x}}$��x��0��eΪ��Ȼ�����ĵ���������x�ķ���$\sqrt{f��x��}$+$\frac{2}{\sqrt{f��x��}}$-��=0���ĸ�����ʵ������ʵ���˵�ȡֵ��Χ�ǣ�������
| A�� | ��0��$\frac{2}{e}$�� | B�� | ��2$\sqrt{2}$��+�ޣ� | C�� | ��e+$\frac{2}{e}$��+�ޣ� | D�� | ��$\frac{{e}^{2}}{2}$+$\frac{4}{{e}^{2}}$��+�ޣ� |
6����֪����f��x��=$\left\{\begin{array}{l}{\frac{1}{x}��x��0}\\{\frac{lnx}{x}��x��0}\end{array}\right.$��������F��x��=f��x��-kx��R����3����㣬��ʵ��k��ȡֵ��ΧΪ��������
| A�� | ��0��$\frac{1}{e}$�� | B�� | ��0��$\frac{1}{2e}$�� | C�� | ��-�ޣ�$\frac{1}{2e}$�� | D�� | ��$\frac{1}{2e}$��$\frac{1}{e}$�� |


 ��ǰ
��ǰ ���Ϊ
���Ϊ ����
���� ��
�� ����
���� �� ��
�� �� �Ķ�����Ϊ�� ��
�Ķ�����Ϊ�� �� B.
B. C.
C. D.
D.
 ����
���� ��ֵ��__________.
��ֵ��__________. ͼ�������е�ĺ������쳤��ԭ����2���������겻�䣩���ٰ�ͼ�������еĵ�����ƽ��1����λ���õ�����
ͼ�������е�ĺ������쳤��ԭ����2���������겻�䣩���ٰ�ͼ�������еĵ�����ƽ��1����λ���õ����� ��ͼ������
��ͼ������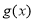 �ĵ����ݼ������ǣ� ��
�ĵ����ݼ������ǣ� ��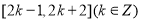 B.
B.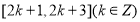
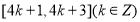 D.
D.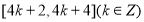
 ������
������ ��ʹ
��ʹ ��������
�������� �� ��
�� �� B��
B��
 D��
D��