题目内容
9.在△ABC中,点D在BC上,∠A=60°,若$\overrightarrow{AD}$=k($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$)=$\frac{1}{4}$$\overrightarrow{AC}$+$λ\overrightarrow{AB}$,且AB=4,则AD的长为3$\sqrt{3}$.分析 设$\overrightarrow{AE}$=$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,$\overrightarrow{AG}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,运用平行四边形法则,可得|$\overrightarrow{AF}$|=$\sqrt{3}$,|$\overrightarrow{AD}$|=$\sqrt{3}$k,再由向量共线定理和平面向量基本定理,可得λ=$\frac{3}{4}$,k=3,即可得到所求值.
解答 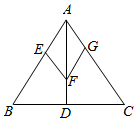 解:设$\overrightarrow{AE}$=$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,$\overrightarrow{AG}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,
解:设$\overrightarrow{AE}$=$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,$\overrightarrow{AG}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,
可得|$\overrightarrow{AE}$|=|$\overrightarrow{AG}$|=1,∠EAF=∠GAF=30°,
即有|$\overrightarrow{AF}$|=$\sqrt{3}$,
|$\overrightarrow{AD}$|=$\sqrt{3}$k,
又B,D,C共线,可得$\frac{1}{4}$+λ=1,即λ=$\frac{3}{4}$,
由k($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$)=$\frac{1}{4}$$\overrightarrow{AC}$+$\frac{3}{4}$$\overrightarrow{AB}$,
可得$\frac{k}{4}$=$\frac{3}{4}$,即k=3,
则|$\overrightarrow{AD}$|=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题考查向量的模的求法,注意运用向量的平行四边形法则和向量共线的定理,以及平面向量基本定理,属于中档题.

 名校课堂系列答案
名校课堂系列答案
| A. | $\frac{1}{4}$ab | B. | $\frac{1}{4}$bc | C. | $\frac{1}{2}$bc | D. | $\frac{1}{2}$ac |
