题目内容
根据反比例函数图象,利用平移直接作出下列函数图象,并求出其在1≤x≤5的最大值和最小值.
(1)y=-
;
(2)y=-
-1;
(3)y=
.
(1)y=-
| 1 |
| x+2 |
(2)y=-
| 1 |
| x-1 |
(3)y=
| 3x+1 |
| x-2 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:根据函数图象的平移变换法则,分析出函数在1≤x≤5时单调性,进而可得在1≤x≤5时最值.
解答:
解:(1)y=-
的图象由y=
的图象向左平移两个单位得到,

故当1≤x≤5时,函数为增函数,
∴当x=1时,函数取最小值-
,当x=5时,函数取最大值-
;
(2)y=-
-1的图象由y=
的图象向右平移一个单位,再向下平移一个单位得到,

故当1≤x≤5时,函数为增函数,
∴函数无最小值,当x=5时,函数取最大值-
;
(3)y=
=
+3的图象由y=
的图象向右平移两个单位,再向上平移三个单位得到,

故当1≤x<2和2<x≤5时,函数均为减函数,
此时函数即无最大值,也无最小值.
| 1 |
| x+2 |
| -1 |
| x |

故当1≤x≤5时,函数为增函数,
∴当x=1时,函数取最小值-
| 1 |
| 3 |
| 1 |
| 7 |
(2)y=-
| 1 |
| x-1 |
| -1 |
| x |

故当1≤x≤5时,函数为增函数,
∴函数无最小值,当x=5时,函数取最大值-
| 5 |
| 4 |
(3)y=
| 3x+1 |
| x-2 |
| 7 |
| x-2 |
| 7 |
| x |

故当1≤x<2和2<x≤5时,函数均为减函数,
此时函数即无最大值,也无最小值.
点评:本题考查的知识点是反比例函数的图象和性质,函数图象的平移变换法则,熟练掌握反比例函数的图象和性质是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
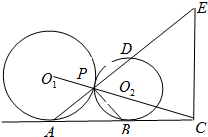 如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2 的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上.
如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2 的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上.