题目内容
10.设a,b,c为正实数,且a+b+c=1,证明:$\frac{1}{ab+2{c}^{2}+2c}$+$\frac{1}{bc+2{a}^{2}+2a}$+$\frac{1}{ca+2{b}^{2}+2b}$≥$\frac{1}{ab+bc+ca}$.分析 首先证明$\frac{ab+bc+ca}{ab+2{c}^{2}+2c}$≥$\frac{ab}{ab+bc+ca}$,①展开后,由2abc(a+b+c)=2abc,由均值不等式可得b2c2+c2a2≥2abc2,可得;$\frac{ab+bc+ca}{bc+2{a}^{2}+2a}$≥$\frac{bc}{ab+bc+ca}$,②,$\frac{ab+bc+ca}{ca+2{b}^{2}+2b}$≥$\frac{ca}{ab+bc+ca}$,③,由累加法即可得证.
解答 证明:首先证明$\frac{ab+bc+ca}{ab+2{c}^{2}+2c}$≥$\frac{ab}{ab+bc+ca}$,①
事实上,上述不等式等价为
a2b2+b2c2+c2a2+2abc(a+b+c)≥a2b2+2abc2+2abc,
由已知可得2abc(a+b+c)=2abc,
由均值不等式可得b2c2+c2a2≥2abc2,
故上述不等式成立.
同理可得$\frac{ab+bc+ca}{bc+2{a}^{2}+2a}$≥$\frac{bc}{ab+bc+ca}$,②
$\frac{ab+bc+ca}{ca+2{b}^{2}+2b}$≥$\frac{ca}{ab+bc+ca}$,③
①+②+③,可得$\frac{ab+bc+ca}{ab+2{c}^{2}+2c}$+$\frac{ab+bc+ca}{bc+2{a}^{2}+2a}$+$\frac{ab+bc+ca}{ca+2{b}^{2}+2b}$≥1,
即有$\frac{1}{ab+2{c}^{2}+2c}$+$\frac{1}{bc+2{a}^{2}+2a}$+$\frac{1}{ca+2{b}^{2}+2b}$≥$\frac{1}{ab+bc+ca}$.
点评 本题考查不等式的证明,注意运用基本不等式和累加法,考查推理能力,是难题.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案| A. | 30° | B. | 120° | C. | 60° | D. | 150° |
| A. | 43 | B. | -3 | C. | 2 | D. | 3 |
| A. | {x|x≥-3} | B. | {x|x≤4} | C. | {x|-3≤x≤4} | D. | {x|x≤-3或x≥4} |
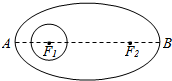 1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.
1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.