题目内容
19.设m,n是两条不同的直线,α,β,γ是三个不同的平面,则以下四个命题:①$\left.\begin{array}{l}{α∥β}\\{α∥β}\end{array}\right\}$⇒β∥γ;②$\left.\begin{array}{l}{α⊥β}\\{α∥β}\end{array}\right\}$⇒m⊥β③$\left.\begin{array}{l}{m⊥α}\\{m∥β}\end{array}\right\}$⇒α⊥β④$\left.\begin{array}{l}{m∥n}\\{n⊆α}\end{array}\right\}$⇒m∥α.
其中正确的命题为( )
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ②④ |
分析 由面面平行的判定定理得①正确;在②中,m与β相交、平行或m?β;由面面垂直的判定定理得③正确;在④中,m∥α或m?α.
解答 解:由m,n是两条不同的直线,α,β,γ是三个不同的平面,知:
在①中,$\left.\begin{array}{l}{α∥β}\\{α∥β}\end{array}\right\}$⇒β∥γ,由面面平行的判定定理得①正确;
在②中,$\left.\begin{array}{l}{α⊥β}\\{α∥β}\end{array}\right\}$⇒m与β相交、平行或m?β,故②错误;
在③中,$\left.\begin{array}{l}{m⊥α}\\{m∥β}\end{array}\right\}$⇒α⊥β,由面面垂直的判定定理得③正确;
在④中,$\left.\begin{array}{l}{m∥n}\\{n⊆α}\end{array}\right\}$⇒m∥α或m?α,故④错误.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
9.已知f(x)=sin(ωx+$\frac{π}{4}$)(ω>0),若f($\frac{π}{2}$)=f(π),且在区间($\frac{π}{2}$,π)内,f(x)≤f($\frac{π}{2}$),则ω=( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{1+8k}{3}$,k∈N | D. | $\frac{5+8k}{3}$,k∈N |
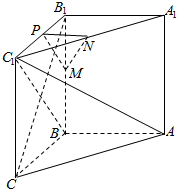 如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=CC1,M、N、P分别是BB1、A1C1、B1C1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=CC1,M、N、P分别是BB1、A1C1、B1C1的中点.