题目内容
已知函数h(x)=
,(a∈R)
(Ⅰ)求函数h(x)的最小值.
(Ⅱ)当a=-1时,求证:
+
+…+
>ln(n+1),(n∈N*).
|
(Ⅰ)求函数h(x)的最小值.
(Ⅱ)当a=-1时,求证:
| 22 |
| 1 |
| 32 |
| 22 |
| (n+1)2 |
| n2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,不等式的证明
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,利用函数最值和导数之间的关系,即可求函数h(x)的最小值.
(Ⅱ)当a=-1时,根据函数h(x)=x2-lnx的单调性,利用函数单调性的性质即可证明不等式.
(Ⅱ)当a=-1时,根据函数h(x)=x2-lnx的单调性,利用函数单调性的性质即可证明不等式.
解答:
解:(Ⅰ)当x≤0时,函数h(x)=x2单调递减,
所以函数h(x)在(-∞,0]上的最小值为h(0)=0
当x>0,h(x)=x2+alnx
若a=0,函数h(x)=x2在(0,+∞)上单调递
此时,函数h(x)不存在最小值
若a>0,因为h′(x)=2x+
=
>0
所以函数h(x)=x2+alnx在(0,+∞)上单调递增
此时,函数h(x)不存在最小值
若a<0,因为h′(x)=
=
所以函数h(x)=x2+alnx在(0,
)上单调递减
在(
,+∞)上单调递增
此时,函数h(x)的最小值为h(
)
因为h(
)=-
+aln
=-
+
ln(-
)=-
[1-ln(-
)]
所以当-2e≤a<0时,h(
)≥0
当a<-2e时,h(
)<0
综上可知,当a>0时,函数h(x)没有最小值
当-2e≤a<0时,函数h(x)的最小值为h(0)=0
当a<-2e时,函数h(x)的最小值为h(
)=-
[1-ln(-
)]
(Ⅱ)当a=-1时,由(Ⅱ)知h(x)=x2-lnx在(1,+∞)为增函数?x>1,h(x)>h(1)=1,
所以x2-lnx>1>0,即x2>lnx
令x=
=1+
>1,
所以(
)2>ln(
),
所以
+
+
+…+
>ln(
…
)=ln(n+1).
所以函数h(x)在(-∞,0]上的最小值为h(0)=0
当x>0,h(x)=x2+alnx
若a=0,函数h(x)=x2在(0,+∞)上单调递
此时,函数h(x)不存在最小值
若a>0,因为h′(x)=2x+
| a |
| x |
| 2x2+a |
| x |
所以函数h(x)=x2+alnx在(0,+∞)上单调递增
此时,函数h(x)不存在最小值
若a<0,因为h′(x)=
| 2x2+a |
| x |
2(x+
| ||||||||
| x |
所以函数h(x)=x2+alnx在(0,
-
|
在(
-
|
此时,函数h(x)的最小值为h(
-
|
因为h(
-
|
| a |
| 2 |
-
|
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
所以当-2e≤a<0时,h(
-
|
当a<-2e时,h(
-
|
综上可知,当a>0时,函数h(x)没有最小值
当-2e≤a<0时,函数h(x)的最小值为h(0)=0
当a<-2e时,函数h(x)的最小值为h(
-
|
| a |
| 2 |
| a |
| 2 |
(Ⅱ)当a=-1时,由(Ⅱ)知h(x)=x2-lnx在(1,+∞)为增函数?x>1,h(x)>h(1)=1,
所以x2-lnx>1>0,即x2>lnx
令x=
| n+1 |
| n |
| 1 |
| n |
所以(
| n+1 |
| n |
| n+1 |
| n |
所以
| 22 |
| 1 |
| 32 |
| 22 |
| 42 |
| 32 |
| (n+1)2 |
| n2 |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
点评:本题主要考查函数单调性最值和导数之间的关系,以及利用导数证明不等式,综合性较强,难度较大.

练习册系列答案
相关题目
已知四棱锥P-ABCD中,底面ABCD是正方形,PA=AD=2,PA⊥平面ABCD,E,F分别是线段AB,BC的中点,则PE与FD所成角的余弦值为( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
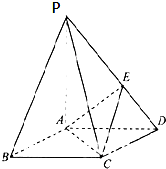 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=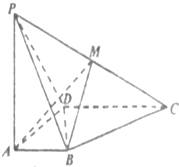 如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.