题目内容
3.若f(x)=$\frac{\sqrt{{a}^{2}-{x}^{2}}}{|x+a|-a}$是奇函数,则实数a的取值范围为(0,+∞).分析 由f(x)是奇函数得到f(-x)=-f(x),由此可以得到|x+a|+|a-x|=2a>0,所以a得范围是(0,+∞).
解答 解:∵f(x)=$\frac{\sqrt{{a}^{2}-{x}^{2}}}{|x+a|-a}$是奇函数,
∴f(-x)=-f(x),即$\frac{\sqrt{{a}^{2}-{x}^{2}}}{|a-x|-a}$=-$\frac{\sqrt{{a}^{2}-{x}^{2}}}{|x+a|-a}$,
∴|x+a|-a=a-|a-x|,
∴|x+a|+|a-x|=2a>0,
∴a>0,
故答案为:(0,+∞).
点评 本题考查由f(x)是奇函数得到f(-x)=-f(x),由此可以得到|x+a|+|a-x|=2a>0,所以a得范围是(0,+∞).

练习册系列答案
相关题目
14.从甲、乙两品种的棉花中各抽测了10根棉花的纤维长度(单位:mm),所得数据如图茎叶图.记甲、乙两品种棉花的纤维长度的平均值分别为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,标准差分别为s甲,s乙,则( )
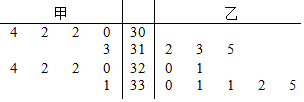

| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲>s乙 | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲<s乙 | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲>s乙 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲<s乙 |
11.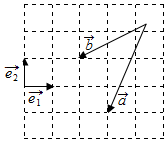 如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )
如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )
 如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )
如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )| A. | 2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B. | 3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | C. | 2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ | D. | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ |
15.下列在实数域上定义的函数中,是奇函数的是( )
| A. | y=x3sinx | B. | y=x2-sinx | C. | y=2x+2 | D. | y=xcosx |
6.已知an=$\frac{2}{n(n+1)}$,则数列{an}的前100项和S100=( )
| A. | $\frac{100}{101}$ | B. | $\frac{200}{101}$ | C. | $\frac{99}{100}$ | D. | $\frac{198}{100}$ |
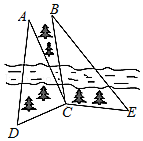 如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;