题目内容
13.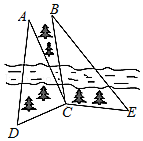 如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;∠ACD=90°,∠ADC=60°,∠ACB=30°,∠BCE=105°,∠CEB=45°,DC=CE=2(百米).
(1)求△CDE的面积;
(2)求A,B之间的距离.
分析 (1)利用周角定义求出∠DCE度数,再由CD与CE的长,利用三角形面积公式求出三角形CDE面积即可;
(2)连接AB,在直角三角形ACD中,利用锐角三角函数定义求出AC的长,在直角三角形BCE中,求出∠CBE度数,利用正弦定理求出BC的长,在三角形ABC中,利用余弦定理求出AB的平方即可.
解答 解:(1)在△CDE中,∠DCE=360°-90°-30°-105°=135°,
∴S△CDE=$\frac{1}{2}$CD•CE•sin135°=$\frac{1}{2}$×2×2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$(平方百米);
(2)连接AB,
根据题意知,在Rt△ACD中,AC=DC•tan∠ADC=2×tan60°=2$\sqrt{3}$(百米),
在△BCE中,∠CBE=180°-∠BCE-∠CEB=180°-105°-45°=30°,
由正弦定理得$\frac{BC}{sin∠CEB}$=$\frac{CE}{sin∠CBE}$,代入求得BC=2$\sqrt{2}$(百米),
在△ABC中,由余弦定理得:AB2=AC2+BC2-2AC•BCcos∠ACB,
则AB2=12+8-2×2$\sqrt{3}$×2$\sqrt{2}$•$\frac{\sqrt{3}}{2}$=20-12$\sqrt{2}$,
∴AB=2$\sqrt{5-3\sqrt{2}}$.
点评 此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.已知函数f(x)=2x-2,g(x)=ax(x-2a)同时满足条件:①?x∈R,f(x)<0或g(x)<0;②?x∈(-∞,-4),使得f(x)g(x)<0,则实数a的取值范围是( )
| A. | (-2,0) | B. | (-∞,-2) | C. | (-8,0) | D. | (0,2) |
2.命题p:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点,则下列表述正确的是( )
| A. | p是假命题,其否定是:?k∈(2,+∞),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点 | |
| B. | p是真命题,其否定是:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| C. | p是假命题,其否定是:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| D. | p是真命题,其否定是:?k∈(2,+∞),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 |