题目内容
在三角形中，三个内角A．B．C成等差数列，三边a．b．c成等比数列，b=4，那么三角形的面积是 ．
考点：正弦定理
专题：解三角形
分析：利用等差、等比中项的性质列出关系式，确定出B与ac的值，利用三角形面积公式即可求出三角形ABC面积．
解答：
解：因为A，B，C成等差数列，所以2B=A+C，
由A+B+C=π得，B=
，
因为a，b，c成等比数列，且b=4，所以b2=ac=16，
则三角形的面积S△ABC=
acsinB=
×16×
=4
，
故答案为：4
．
由A+B+C=π得，B=
| π |
| 3 |
因为a，b，c成等比数列，且b=4，所以b2=ac=16，
则三角形的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故答案为：4
| 3 |
点评：本题考查等差、等比中项的性质，以及三角形面积公式，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
幂函数的图象过点（2，8），则它的单调递增区间是（ ）
| A、（0，+∞） |
| B、[0，+∞） |
| C、（-∞，0） |
| D、（-∞，+∞） |
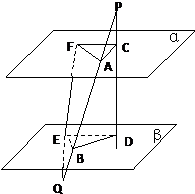如图，线段PQ分别交两个平行平面α、β于A、B两点，线段PD分别交α、β于C、D两点，线段QF分别交α、β于F、E两点，若PA=9，AB=12，BQ=12，△ACF的面积为72，求△BDE的面积．在四面体PABC中，PA、PB、PC两两垂直，且均相等，E是AB的中点，则异面直线AC与PE所成的角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|