题目内容
12.若用二分法求函数f(x)在(a,b)内的唯一零点时,精确度为0.001,则结束计算的条件是$\frac{b-a}{{2}^{n}}$<0.001.分析 精确度是方程近似解的一个重要指标,它由计算次数决定.若初始区间是(a,b),那么经过1次取中点后,区间的长度是$\frac{b-a}{2}$,…,经过n次取中点后,区间的长度是$\frac{b-a}{{2}^{n}}$,
解答 解:设至少需要计算n次,则n满足$\frac{b-a}{{2}^{n}}$<0.001,
故结束计算的条件是:$\frac{b-a}{{2}^{n}}$<0.001,
故答案为:$\frac{b-a}{{2}^{n}}$<0.001
点评 本题考查二分法求方程的近似解,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
2.两个正数a、b的等差中项是$\frac{7}{2}$,一个等比中项是2$\sqrt{3}$,且a<b,则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
3.直线l与抛物线y2=6x交于A,B两点,圆(x-6)2+y2=r2与直线l相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
| A. | ($\sqrt{3}$,2$\sqrt{3}$) | B. | ($\sqrt{3}$,3$\sqrt{3}$) | C. | (3,$2\sqrt{3}$) | D. | (3,3$\sqrt{3}$) |
7.已知可导函数f(x)(x∈R)的导数f′(x)满足f′(x)-f(x)<0,则( )
| A. | ef(2015)>f(2016) | B. | ef(2015)<f(2016) | ||
| C. | ef(2015)=f(2016) | D. | ef(2015)与f(2016)的大小不确定 |
17.已知$cos(\frac{π}{6}-x)=-\frac{{\sqrt{3}}}{3}$,则$cos(\frac{5π}{6}+x)+sin(\frac{2π}{3}-x)$=( )
| A. | $-\sqrt{3}$ | B. | -1 | C. | 0 | D. | $\sqrt{3}$ |
4.函数f(x)=x2-f'(-1)x+1在x=1处的切线方程为( )
| A. | y=-x+4 | B. | y=3x | C. | y=3x-3 | D. | y=3x-9 |
2.下列选项中方程表示图中曲线的是( )
| A. |  x2+y2=1 | B. |  x2-y2=0 | C. |  y=|x| | D. |  lgx+lgy=0 |
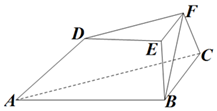 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.