题目内容
17.已知$cos(\frac{π}{6}-x)=-\frac{{\sqrt{3}}}{3}$,则$cos(\frac{5π}{6}+x)+sin(\frac{2π}{3}-x)$=( )| A. | $-\sqrt{3}$ | B. | -1 | C. | 0 | D. | $\sqrt{3}$ |
分析 根据三角函数的诱导公式,进行化简计算即可.
解答 解:∵$cos(\frac{π}{6}-x)=-\frac{{\sqrt{3}}}{3}$,
∴$cos(\frac{5π}{6}+x)+sin(\frac{2π}{3}-x)$
=cos[π-($\frac{π}{6}$-x)]+sin[$\frac{π}{2}$+($\frac{π}{6}$-x)]
=-cos($\frac{π}{6}$-x)+cos($\frac{π}{6}$-x)
=0.
故选:C.
点评 本题考查了三角函数的诱导公式与应用问题,是基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
5.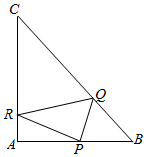 在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
 在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
2.曲线y=4x-x3,在点(-1,-3)处的切线方程是( )
| A. | y=7x+4 | B. | y=x-4 | C. | y=7x+2 | D. | y=x-2 |
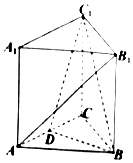 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.