题目内容
设数列{an}满足:a1=1,an+1=3an,n∈N*
(Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)已知数列{bn}是等差数列,Tn为{bn}的前n项和,且b1=a1+a2+a3,b3=a3,求Tn的最大值.
(Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)已知数列{bn}是等差数列,Tn为{bn}的前n项和,且b1=a1+a2+a3,b3=a3,求Tn的最大值.
考点:等比数列的前n项和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知可得{an}是首项为1,公比为3的等比数列,然后直接利用等比数列的通项公式和前n项和得答案;
(Ⅱ)由(Ⅰ)中的通项公式和前n项和求得等差数列{bn}的公差d,代入等差数列的前n项和公式后利用二次函数求得最值.
(Ⅱ)由(Ⅰ)中的通项公式和前n项和求得等差数列{bn}的公差d,代入等差数列的前n项和公式后利用二次函数求得最值.
解答:
(Ⅰ)由a1=1,an+1=3an,
可得{an}是首项为1,公比为3的等比数列,
∴an=3n-1,
Sn=
=
(3n-1);
(Ⅱ)由b1=a1+a2+a3=S3=
(33-1)=13,b3=9,
得等差数列{bn}的公差d=
=
=-2,
∴Tn=13n+
×(-2)=-n2+14n.
当n=7时,Tn有最大值49.
可得{an}是首项为1,公比为3的等比数列,
∴an=3n-1,
Sn=
| 1×(1-3n) |
| 1-2 |
| 1 |
| 2 |
(Ⅱ)由b1=a1+a2+a3=S3=
| 1 |
| 2 |
得等差数列{bn}的公差d=
| b3-b1 |
| 2 |
| 9-13 |
| 2 |
∴Tn=13n+
| n(n-1) |
| 2 |
当n=7时,Tn有最大值49.
点评:本题考查了等比数列的通项公式,考查了等比数列的前n项和,考查了等差数列的性质,训练了二次函数最值的求法,是基础的计算题.

练习册系列答案
相关题目
当a=3时,下面的程序段输出的y是( )


| A、9 | B、3 | C、10 | D、6 |
一个四棱锥的三视图如图所示,则该四棱锥的侧面中,直角三角形的个数为( )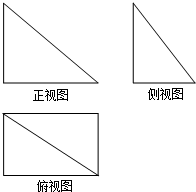

| A、1 | B、2 | C、3 | D、4 |
已知各项均为正数的等比数列{an}中,3a1,
a3,2a2成等差数列
=( )
| 1 |
| 2 |
| a11-a13 |
| a8-a10 |
| A、27 | B、1 |
| C、-1 | D、-1或27 |
已知函数f(x)=x+
,则函数y=f(x)的大致图象为( )
| 1 |
| |x| |
A、 |
B、 |
C、 |
D、 |