题目内容
6.已知焦点在x轴双曲线的一条渐近线的倾斜角$\frac{π}{6}$,则此双曲线的离心率为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 设出双曲线方程,列出关系式,即可求解双曲线的离心率.
解答 解:设双曲线方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,依题意 $\frac{b}{a}=\frac{{\sqrt{3}}}{3}$,$\frac{{\sqrt{{c^2}-{a^2}}}}{a}=\frac{{\sqrt{3}}}{3}$,$e=\frac{{2\sqrt{3}}}{3}$.
故选:D.
点评 本题考查双曲线的简单性质的应用,离心率的求法,考查计算能力.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
17.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),若(k$\overrightarrow{a}+\overrightarrow{b}$)⊥(3$\overrightarrow{a}-\overrightarrow{b}$),则实数k=( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
14.如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )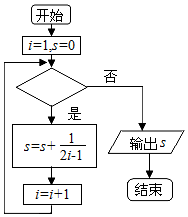

| A. | i≤1008? | B. | i>1008? | C. | i≤1009? | D. | i>1009? |
10.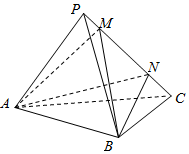 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
17.执行如图所示的程序框图,则输出的S等于( )
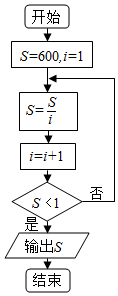

| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
14.由曲线y=$\sqrt{x}$,直线y=x所围成的封闭曲线的面积是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |