题目内容
已知数列{an}满足:a1=1,a2=a(a≤1),an+2=|an+1-an|,当a4=1时,a10的值为( )
| A、0 | B、1 | C、0或1 | D、±1 |
考点:数列递推式
专题:等差数列与等比数列
分析:由a≤1,an+2=|an+1-an|,a1=1,a2=a,可得a3=|a2-a1|=|a-1|=1-a,a4=|a3-a2|=|1-2a|,由题设知a4=|1-2a|=1,所以a=1,或a=0.进而根据an+3=an成立,可得答案.
解答:
解:∵a≤1,an+2=|an+1-an|,a1=1,a2=a,
∴a3=|a2-a1|=|a-1|=1-a,
a4=|a3-a2|=|1-2a|,
又∵a4=|1-2a|=1,
∴a=1,或a=0.
经检验无论a=1,还是a=0,
都有an+3=an成立,
于是a10=a7=a4=1,
故选:B
∴a3=|a2-a1|=|a-1|=1-a,
a4=|a3-a2|=|1-2a|,
又∵a4=|1-2a|=1,
∴a=1,或a=0.
经检验无论a=1,还是a=0,
都有an+3=an成立,
于是a10=a7=a4=1,
故选:B
点评:本题考查了递推数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
数列{an}满足递推公式an=3an-1+3n-1(n≥2),又a1=5,则使得{
}为等差数列的实数λ=( )
| an+λ |
| 3n |
| A、2 | ||
| B、5 | ||
C、-
| ||
D、
|
18×17×16×…×9×8等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
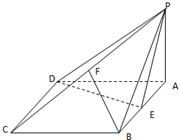 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.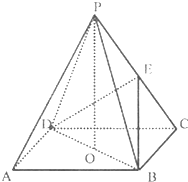 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.