题目内容
12.用分析法证明:已知a,b∈R且a≠b,则$|\frac{1}{{a}^{2}+1}-\frac{1}{{b}^{2}+1}|<|a-b|$.分析 寻找使:$|\frac{1}{{a}^{2}+1}-\frac{1}{{b}^{2}+1}|<|a-b|$成立的充分条件,直到使不等式成立的条件显然具备.
解答 证明:要证明$|\frac{1}{{a}^{2}+1}-\frac{1}{{b}^{2}+1}|<|a-b|$
只要证明|$\frac{(b-a)(b+a)}{({a}^{2}+1)({b}^{2}+1)}$|<|a-b|,而a,b∈R且a≠b,
故把|a-b|约分,只要证明|$\frac{b+a}{({a}^{2}+1)({b}^{2}+1)}$|<1
即证|a+b|<(a2+1)(b2+1)
显然a和b同号时|a+b|较大,所以不妨设a>0,b>0
只要证明a+b<a2b2+a2+b2+1
因为a2-a+$\frac{1}{4}$=(a-$\frac{1}{2}$)2,b2-b+$\frac{1}{4}$=(b-$\frac{1}{2}$)2,
所以a2-a+b2-b+1>0 a2b2≥0
所以a>0,b>0时,a+b<a2b2+a2+b2+1成立.
故$|\frac{1}{{a}^{2}+1}-\frac{1}{{b}^{2}+1}|<|a-b|$.
点评 本题主要考查用分析法证明不等式,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
2.已知b<a<0,$\root{3}{a}$-$\root{3}{b}$=m,$\root{3}{a-b}$=n,则有( )
| A. | m>n | B. | m<n | C. | m=n | D. | m≤n |
2.若θ在第四象限,则sin(cosθ)•cos(sinθ)的值为( )
| A. | 正值 | B. | 负值 | C. | 零 | D. | 以上都有可能 |
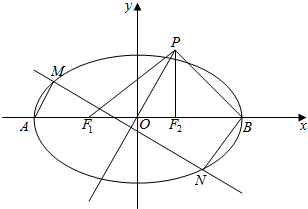 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别是F1,F2,左、右顶点分别为A、B,焦距为2c,O为坐标原点,点P(c,b)满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别是F1,F2,左、右顶点分别为A、B,焦距为2c,O为坐标原点,点P(c,b)满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$.