题目内容
20.如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙.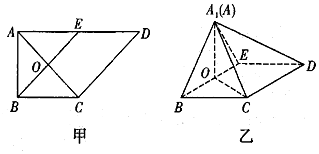
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求BC与平面A1CD所成的角.
分析 (1)根据线面垂直的判定定理即可证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,利用等体积即可求BC与平面A1CD所成的角..
解答 (1)证明:在图甲中,∵AB=BC=1,AD=2,E是AD的中点,∠BAD=$\frac{π}{2}$,
∴BE⊥AC,即在图乙中,BE⊥OA1,BE⊥OC.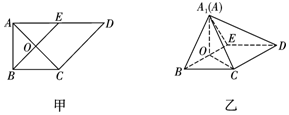
又OA1∩OC=O,∴BE⊥平面A1OC.
∵BC∥DE,BC=DE,
∴BCDE是平行四边形,
∴CD∥BE,∴CD⊥平面A1OC. …(6分)
(2)解:由题意,CD=BE=$\sqrt{2}$,平面A1BE⊥平面BCDE,
∴OA1⊥平面BCDE,∴OA1⊥OC
∴A1C=1
∵BE⊥平面A1OC,∴BE⊥A1C
∵CD∥BE,∴CD⊥A1C.
设B到平面A1CD的距离为d,
由∴$\frac{1}{3}×\frac{1}{2}×1×\sqrt{2}d=\frac{1}{3}×\frac{1}{2}×1×\sqrt{2}sin\frac{3π}{4}×\frac{\sqrt{2}}{2}$,
∴d=$\frac{1}{2}$,故B到平面A1CD的距离为$\frac{1}{2}$,
∴BC与平面A1CD所成的角为30°. …(12分)
点评 本题考查了平面立体转化的问题,运用好折叠之前,之后的图形,对于空间直线平面的位置关系的定理要很熟练.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知A、B是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,若在双曲线上存在点P满足2|$\overrightarrow{PA}$+$\overrightarrow{PB}$|≤|$\overrightarrow{AB}$|,则双曲线C的离心率e的取值范围是( )
| A. | 1<e≤2 | B. | e≥2 | C. | 1<e≤$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
11.正三棱柱ABC-A1B1C1中,若AC=$\sqrt{2}$AA1,则AB1与CA1所成角的大小为( )
| A. | 60° | B. | 105° | C. | 75° | D. | 90° |
10.若实数x,y满足约束条件$\left\{\begin{array}{l}{x+2y-4≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$,则$\frac{y}{x-3}$的最小值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | -2 |
 如图,棱长为2的正方体ABCD-A1B1C1D1中,P为A1B1的中点
如图,棱长为2的正方体ABCD-A1B1C1D1中,P为A1B1的中点