题目内容
9.设函数f(x)=2cos2ωx-1(ω>0),将y=f(x)的图象向右平移$\frac{π}{3}$个单位长度后,所得图象与原图角重合,则ω的最小值等于( )| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
分析 根据函数y=Asin(ωx+φ)的图象变换规律,可得 $\frac{2ωπ}{3}$=2kπ,k∈Z,求得ω的最小值.
解答 解:将y=f(x)=2cos2ωx-1=cos2ωx的图象向右平移$\frac{π}{3}$个单位长度后,可得y=cos2ω(x-$\frac{π}{3}$)的图象,
再根据所得图象与原图角重合,则有 $\frac{2ωπ}{3}$=2kπ,k∈Z,则ω的最小值等于3,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
1.已知$cos\frac{4π}{5}cos\frac{7π}{15}+sin\frac{4π}{5}sin\frac{7π}{15}$=$\frac{2}{3}+cos(\frac{π}{2}+x)cosx$则sin2x等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{12}$ | D. | -$\frac{1}{12}$ |
18.若实数x,y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$则z=-$\frac{5}{4x+3y}$的最大值为( )
| A. | -$\frac{15}{8}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{1}{2}$ | D. | -1 |
19.已知{an}是等差数列,a3+a11=40,则a6-a7+a8等于( )
| A. | 20 | B. | 48 | C. | 60 | D. | 72 |
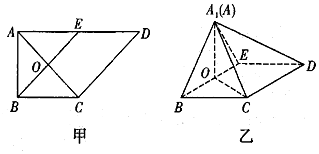
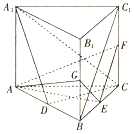 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F、G分别是BC、CC1、BB1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F、G分别是BC、CC1、BB1的中点.